A.9. Apéndice 1: Complementos de geometría. 

A lo largo del texto de nivel introductorio (nivel A) hemos manejado conceptos geométricos en dos aspectos muy distintos. Por una parte hemos introducido una imagen de un espacio y un tiempo relativos e intercambiables que creemos que reflejan bastante bien los cambios que introdujo la Relatividad en la ciencia y en nuestra visión del mundo. Y por otra hemos usado la geometría elemental para presentar los razonamientos que sustentan la teoría sin necesitar cálculos matemáticos.

De hecho a lo largo del texto no aparece más que una fórmula, la famosa ecuación de la energía de Einstein, y aparece en las primeras páginas (apartados A.1.1 y A.2.3) como cita histórica y sin relacionarla con ningún cálculo y en el capítulo A.8 que trata sobre el significado de esta ecuación.

Para eludir el cálculo matemático nos hemos apoyado únicamente en tres elementos: la tabla 1 (apartado A.4.2) que hemos utilizado para presentar el factor gamma () o constante relativista, el trazado de la diagonal del cuadrado (apartados A.4.6 y A.4.7), que está relacionado con el teorema de Pitágoras, y en tercer lugar los diagramas de Minkowski, el sistema de coordenadas de nuestros gráficos, que ha sido la herramienta fundamental.

La tabla 1 suple el cálculo del factor gamma pero contiene la información fundamental de ese concepto. El que quiera profundizar más en su significado deberá leer el texto de nivel B o cualquier texto equivalente de los muchos que se encuentran en internet o en las librerías.

El trazado de la diagonal del cuadrado no encierra grandes dificultades, y sólo se ha usado como ejemplo concreto fácil de reproducir. Concretamente para ver que la diagonal mide 1,41 veces el lado, es decir, menos de vez y media el lado (menos de 1,5). Con este ejemplo se consigue ver claramente que la luz no puede hacer su recorrido a menos que exista una contracción de longitudes.

Sin embargo la herramienta que hemos usado más extensamente es el sistema de coordenadas del espacio-tiempo de Minkowski, y aunque lo hemos hecho a un nivel muy intuitivo (y sin cálculos) y aunque no dudamos de su valor didáctico, su potencia y su precisión, somos conscientes de pueden resultar el principal escollo para entender los razonamientos expuestos.

Dedicaremos los dos apartados siguientes a dar algunas pistas que pueden facilitar la comprensión de los diagramas de Minkowski.

A.9.1.  El espacio-tiempo congelado en una película

En el texto hemos intentado explicar con claridad como se usan los diagramas de Minkowski, pero posiblemente hayamos perdido su significado profundo entre la complejidad de algunos razonamientos y la dificultad de los nuevos conceptos que trae la Relatividad.

Antes de 2005 y de la R.E. el tiempo era sólo un capítulo de la filosofía y la ciencia no tenía gran cosa que decir sobre esto. Espacio y tiempo eran dos puntos de partida sobre los que se sustentaba la física, pero no se discutían. Para la física estos conceptos se consideraban bien definidos si sabíamos como medirlos con precisión, y los instrumentos de medida habían progresado extraordinariamente.

Sin embargo el experimento de Michelson y Morley, y posteriormente las teorías de Einstein, destruyeron la seguridad que se tenía a finales del siglo XIX en nuestra capacidad de medir estas magnitudes. La medida del espacio y del tiempo dejó de ser objetiva y pasó a ser relativa a la velocidad del observador.

Si el tiempo absoluto anterior a Einstein resultaba difícil de imaginar, el tiempo relativo posterior lo era aun más. Podríamos decir que la Relatividad convirtió un problema filosófico, y por tanto opinable, en un problema físico que necesitaba un análisis y un modelo mucho más sólido para evitar que la física se estancase.

La geometría de Minkowski resolvió el problema aportando un modelo geométrico coherente que encaja como un guante con le R.E. y en el que el concepto de tiempo tiene una representación accesible a nuestra intuición.

Con Minkowski toma forma el concepto de tiempo como cuarta dimensión y sus planteamientos geométricos abrieron el camino de Einstein hacia la R.G. de 1915.

Está claro que el tiempo relativista es uno de los conceptos más importantes introducidos en las páginas anteriores. Podríamos decir sin exagerar que si no se entiende el nuevo concepto de tiempo no se entiende la Relatividad, de manera que ha llegado el momento de recapitular y reflexionar sobre esta cuarta dimensión.

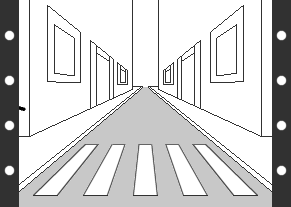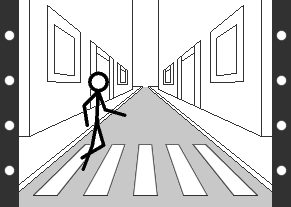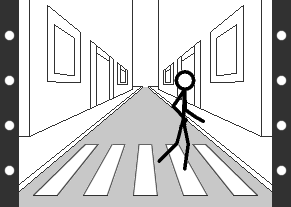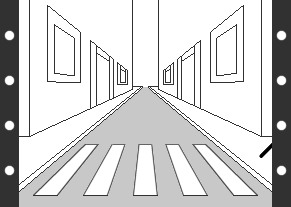
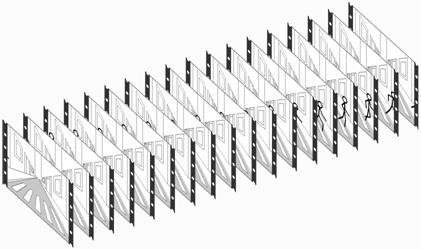
1) El concepto de tiempo está indudablemente ligado al movimiento, de manera que para profundizar en el primero comenzaremos por “capturar el movimiento” para poder analizar sus componentes.

Tras un siglo de cine (1894) está claro que la mejor manera de capturar el movimiento es en una película. Aunque el soporte actual sea digital, el concepto no ha variado desde los hermanos Lumiere, y una película sigue siendo una colección de fotogramas que se proyectan uno tras otro y nos transmiten la sensación de movimiento.

Imaginemos una escena en la que aparezca un movimiento lineal (siguiendo una línea recta), como el de una persona caminando a lo largo de una calle.

Si capturamos una película de este movimiento obtendremos una sucesión de imágenes similares a las que se pueden ver en la figura de la derecha.

Fig. 9.3 -  Una película es una versión

congelada de nuestro pasado.

Las imágenes fotográficas estimulan nuestra memoria y nos permiten recordar hechos pasados, pero una película nos permite “ver” de nuevo aquellos hechos. Podríamos decir que nos transporta a aquella situación.

No tenemos que realizar grandes esfuerzos por recordar porque lo “vemos” de nuevo.

En la Fig. 9.1 se puede ver (en internet) la “película” que resulta de visionar estas 18 imágenes o fotogramas uno tras otro. El movimiento que representan cobra vida incluso aunque los saltos entre imágenes resulten muy palpables.

Fig. 9.1 -  Al ver la sucesión de imágenes el

movimiento cobra vida ante nuestros ojos.

El efecto de la imagen es tan fuerte sobre nosotros que lo que vemos en una película puede pasar a nuestra memoria como si lo hubiéramos vivido, como si hubiéramos estado allí.

2) Para entender el espacio-tiempo de la Relatividad necesitamos hacer un esfuerzo de imaginación para darle a esas imágenes un peso equivalente al de la misma realidad.

 Como primera aproximación podemos suponer que somos la persona que está caminando en nuestra película. Al ver las imágenes nos transportan a una situación que hemos vivido, nos transportan a nuestro pasado.

Si somos esa persona, para nosotros las imágenes de la película resultan muy parecidas al propio pasado. La película es una versión congelada de nuestro pasado.

Tendremos que profundizar en este concepto hasta ver que la propia realidad puede ser muy parecida a esa realidad congelada en una película.

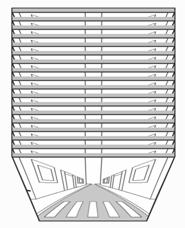
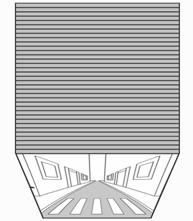
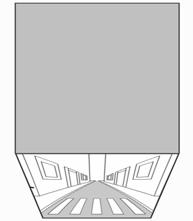
3) Queremos hacer un esfuerzo de imaginación que nos permita ver la película como la misma realidad y no sólo como una imagen de ella.

Para materializar esa idea de realidad congelada comenzamos por recortar los fotogramas de la película y ordenarlos uno tras otro sobre nuestra mesa.

Fig. 9.2 -  Recortamos y ordenamos los fotogramas.

Este paquete de imágenes nos da una nueva visión del movimiento. Vemos como en los sucesivos fotogramas esa persona se va desplazando hacia la derecha hasta “salirse de la foto”, pero también vemos, más claramente que antes, el salto entre un fotograma y el siguiente.

En una película de verdad (en celuloide) las diferencias entre dos fotogramas sucesivos son muy pequeñas ya que se suelen capturar por lo menos 30 imágenes por segundo. Para ver las diferencias deberemos superponer los fotogramas y observar por transparencia estas diferencias.

El hecho de que haya diferencias nos hace pensar que podríamos tomar más imágenes por segundo hasta que no se notasen las diferencias.

Supongamos que tenemos un primer paquete de imágenes a 30 fotogramas por segundo y ponemos a su lado uno con  60 imágenes por segundo. Evidentemente para representar la misma escena obtendremos el doble de imágenes. Si queremos que el paquete no aumente de volumen podemos reducir el grosor del celuloide a la mitad, de manera que el conjunto ocupe el mismo volumen.

Haciendo esto varias veces podemos llegar a tener muchísimos fotogramas en el mismo espacio, hasta que no se noten los saltos de un fotograma al siguiente.

En la realidad la transición entre dos instantes sucesivos es imperceptible. Se dice que la realidad es continua, que en el tiempo real no hay saltos (en mecánica cuántica dudan de esta afirmación, pero no entraremos en este tema).

El último paquete, mucho más tupido, representa mejor esta idea de continuidad del tiempo.

Para nosotros esta sucesión “continua” de fotogramas será la mejor imagen posible del tiempo real.

Quizás aun no resulte evidente lo que queremos decir, así que vamos a jugar por un momento a ser como dioses.

4) En efecto, imaginar el tiempo de esta manera (como un paquete de instantes congelados) es equivalente a adoptar el punto de vista de una deidad.

Desde tiempos ancestrales atribuimos a los dioses capacidades de las que nosotros carecemos, y con frecuencia se espera que alguna deidad o todas ellas puedan viajar por el tiempo o ver simultáneamente el pasado, el presente y el futuro de los humanos.

Incluso muchos humanos creen que tras la muerte se convertirán en algo parecido a esa deidad y por tanto es posible que ellos lleguen a poder realizar estos viajes en el tiempo o al menos a ver simultáneamente el pasado, el presente y el futuro.

Esta idea de poder ver pasado, presente y futuro equivale a decir que la propia realidad está en cierta manera congelada como en nuestro paquete de fotogramas, y nuestra imagen de una deidad que pueda ver a través del tiempo resulta muy parecida a la imagen del humano que puede mirar cualquier fotograma de nuestro paquete.

El espacio tiempo de la Relatividad es similar a imaginar que la propia realidad está en cierta manera congelada y que la estamos observando desde fuera del tiempo, como si fuéramos dioses. Esta imagen es prácticamente idéntica a la del paquete de fotogramas que hacíamos en los apartados anteriores. La diferencia más importante es que allí sólo considerábamos congelado nuestro pasado.

A los humanos no nos suele gustar esta imagen del tiempo porque con frecuencia tenemos la sensación de que conlleva que el futuro también está predeterminado y esto significaría que no existe el libre albedrío, sin embargo la Relatividad sólo es aplicable a un entorno que funcione de forma mecánica, y allí la física (no cuántica) sí prevé que el futuro está completamente predeterminado. Según la física clásica y la Relativista, la situación inicial de las piezas mecánicas que intervienen determina toda su evolución futura.

5) Antes de terminar conviene observar que en nuestro modelo de espacio-tiempo hemos hecho algunas simplificaciones. La más importante consiste en que el universo reflejado en un fotograma es plano, en el sentido de que en él sólo podemos ver lo que ocurre en primer plano. Lo que ocurre dentro de las casas de detrás o lo que ocurre en la calle siguiente no se puede “congelar” en nuestra imagen. En cambio el fotograma de nuestro “dios” sería tridimensional, como una maqueta... o mejor dicho, como la realidad misma.

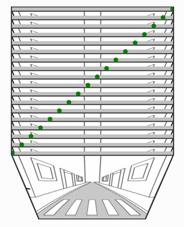
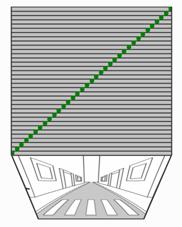
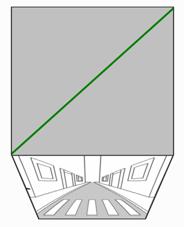
6) Y para terminar veamos que los diagramas de Minkowski son exactamente esta realidad congelada en un paquete de fotogramas.

En la cara superior de los fotogramas (ver Fig. 9.5, 9.6 y 9.7) vemos lo siguiente:

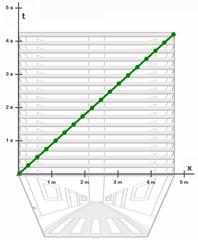
Así pues, mirando nuestro paquete de fotogramas desde arriba estamos viendo de una manera muy parcial la realidad, pero podemos esquematizar lo que pasa en ese trozo de calle a lo largo del tiempo, y podemos analizarlo con bastante precisión.

Si ahora observamos donde está la cabeza del viandante en cada fotograma y lo marcamos con un punto verde en la parte superior de cada fotograma veremos algo parecido a lo que se ve en las figuras 9.8, 9.9. y 9.10.

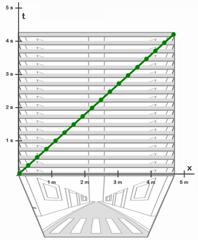
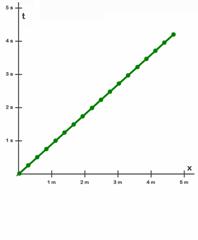
Nuestros fotogramas tenían por si mismos la limitación de ser planos, perdían la tercera dimensión, la profundidad, y al mirar sólo la cara superior de nuestro cubo, nosotros estamos también renunciado a la segunda dimensión, la altura, (figuras 9.11, 9.12 y 9.13) y nos quedamos sólo con una dimensión espacial (la longitud de la calle).

A cambio la sucesión de fotogramas nos da una buena representación para el tiempo, que viene representado por la sucesión de fotogramas. Así el eje vertical representa los sucesivos fotogramas o instantes de tiempo y si los graduamos como tales obtenemos los diagramas de Minkowski.

La línea verde representa la posición de la cabeza en los sucesivos fotogramas, o sea en los sucesivos instantes de tiempo. Es lo que llamábamos la línea de evolución o la línea-mundo de ese objeto.

Nuestros diagramas nunca pueden representar las cuatro dimensiones del espacio-tiempo pues nuestros ojos sólo perciben tres dimensiones, y por tanto sólo con ecuaciones (y posiblemente con la ayuda de un ordenador) podemos tratar problemas complicados en los que todas las dimensiones sean importantes. Esta es la única limitación importante de nuestro modelo geométrico.

7) Sin embargo esto no ha terminado. Sobre esta realidad congelada sólo hemos representado unos ejes del espacio-tiempo, los nuestros. Este sería el concepto de espacio-tiempo de la física clásica, o sea anterior a la Relatividad.

La novedad que aporta la Relatividad, lo verdaderamente difícil, es ver que sobre esta realidad congelada (nuestro cubo de fotogramas) si queremos representar la que se observa desde otro sistema inercial deberemos cortar los fotogramas en otro ángulo, y por tanto la simultaneidad (que viene representada por la idea de fotograma) se ve diferente desde cada sistema.

Con esto en mente se pueden volver a releer las paradojas anteriores y posiblemente encontraremos un concepto de espacio-tiempo mucho más claro y profundo que en la primera lectura.

A.9.2.  Como leer los diagramas de Minkowski

Aunque en el texto hemos explicado el uso de los diagramas y hemos puesto abundantes ejemplos, posiblemente interpretar esos diagramas es la mayor dificultad para entender la Relatividad y seguir los razonamientos expuestos.

Por este motivo comentamos aquí algunas claves para interpretar correctamente los diagramas.

Para evitar que tengamos que girar páginas todo el rato, reproducimos aquí la mayoría de gráficos citados, de manera que resulte fácil seguir el hilo de los razonamientos.

1) Los diagramas permiten representar objetos puntuales y razonar sobre su evolución y sobre como se verán en diferentes sistemas, pero debe quedar claro que están limitados a objetos puntuales.

Cuando hemos hecho razonamientos sobre un cuerpo extenso, como una barra de un metro (apartado A.5.7) o un coche y un garaje (apartado A.6) siempre nos hemos limitado a razonar sobre sus extremos izquierdo y derecho, que son sólo dos puntos, ya que nuestros diagramas de Minkowski sólo representan una dimensión espacial, la x.

Cuando intentamos razonar sobre más de 2 o 3 puntos los diagramas se complican mucho y dejan de ser claros (en las Fig. 6.5 y Fig. 6.6 utilizábamos 4 puntos).

2) Leer la posición de un punto es fácil, pero cuando se está razonando sobre cosas complicadas también es fácil leer mal. Cuando empecemos a encontrar dificultades para interpretar los diagramas convendrá repasar de nuevo el ejemplo sencillo del apartado A.5.5 (Fig. 5.6) en donde se ve como trazar las paralelas a los ejes verdes para leer lo que ve el sistema S’ verde.

Constantemente comparamos lo que ve S con lo que ve S’, así que es imprescindible leer con soltura sobre ambos sistemas, el S negro y el S’ verde.

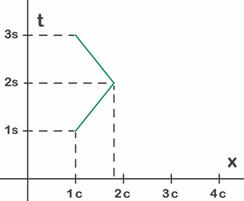
3) Cuando hablamos de la posición de un punto es fácil interpretar que estamos hablando de la posición en el diagrama, pero en general esta interpretación es incorrecta. Sobre los diagramas de Minkowski se representa la posición espacial y el instante temporal de un suceso, así que el término “posición” se refiere a la coordenada espacial y el “instante” a la coordenada temporal.

Al utilizar diagramas de Minkowski se suele utilizar el término “suceso” para los puntos del diagrama. Un suceso es entonces una pareja de datos (posición e instante) y debe interpretarse el punto como “estar en el lugar x en el instante t”. Por esto se dice que los diagramas representan el espacio-tiempo.

Para entender los diagramas es imprescindible tener claro que los sucesos ocurren una sola vez, pero que cada sistema los interpreta de distinta manera, es decir, da unas coordenadas propias, diferentes de las de otro sistema.

4) Dado que utilizamos ejes de espacio y de tiempo un mismo objeto puede aparecer muchas veces, pues podemos representarlo en diferentes instantes de tiempo.

De hecho si representamos el punto en todas las posiciones que va adoptando con el paso del tiempo obtenemos una línea continua (los objetos no dan saltos bruscos a puntos alejados).

En la Fig. 9.14 podemos ver la representación de un objeto que va hacia la derecha y al cabo de un rato cambia y pasa a ir hacia la izquierda.

Fig. 9.14 -  Objeto en movimiento.

Para entenderlo puede ser conveniente buscar las coordenadas de varios puntos del primer segmento, viendo como los sucesivos puntos representan instantes distintos y posiciones que van hacia la derecha.

La evolución temporal de un punto (otra vez sólo de un punto) es, por tanto, una línea continua y se llama línea-mundo de este punto. Este concepto se utiliza en casi todos los diagramas de este texto. Los diagramas de la Fig. 5.7 y siguientes representan la evolución de cada punto por una línea roja. Así la línea roja representa un sólo objeto puntual, pero en muchas posiciones: todas las posiciones por las que pasa a lo largo del tiempo.

5) Para entender los diagramas más complicados (de la Fig. 5.7 en adelante) es necesario saber interpretar el significado de la línea roja y leer sus puntos. Cada punto de la línea roja representa el lugar en el que está el objeto (puntual) en un instante.

Si se encuentran dificultades para usar esos diagramas conviene probar tres tipos de ejercicios.

Primero escoger un punto de la línea roja y buscar sus coordenadas, y después leer otro punto de la misma línea roja (línea-mundo) y comparar si el objeto ha cambiado de posición o de tiempo.

Segundo escoger un instante y buscar la posición del objeto sobre la línea roja, escoger otro instante posterior y buscar de nuevo la posición sobre la línea roja, comparando si se ha movido y hacia donde (sólo se mueve sobre una recta horizontal que representa los raíles del tren).

Tercero escoger una posición y buscar el objeto sobre la línea roja y leer el instante en que se encontraba en esa posición. Podemos encontrarnos con que siempre está en esa posición o que nunca pasa por ella.

6) Para entender los objetos extensos, como las barras de los ejemplos 3 y 4 (A.5.7 y A.5.8), es necesario mirar donde ve los extremos izquierdo y derecho el observador de S (o de S’) y para ello hay que tener en cuenta que miran los puntos por los que ha pasado el objeto (miran sobre la línea-mundo roja) pero eligen el mismo instante para ambos extremos.

Ya hemos hablado de como buscar puntos para un instante determinado, así que con un poco de atención podremos encontrar los dos extremos para el mismo instante. Después unimos con la línea azul (porque los demás puntos de la barra estarán entre los dos extremos) y sabremos como ve la barra ese sistema.

Habrá que repetir el ejercicio en ambos sistemas, pues ambos leen de diferente manera los espacios y los tiempos. Para evitar confusiones en el texto siempre lo hemos hecho en gráficos distintos, pero eso hace más difícil ver que estamos hablando de la misma situación.

Así por ejemplo el diagrama de la Fig. 5.7 y el de la Fig. 5.8 representan la misma situación (las líneas mundo son las mismas) pero vistas por sistemas distintos (observadores distintos). Ven las barras de manera muy diferente porque miran ambos extremos en el mismo instante (simultáneamente) y los dos sistemas ven la simultaneidad de manera muy diferente.