A.7.9. La paradoja de los gemelos, 4^a parte.

Observaciones finales, aceleraciones y Relatividad General

Lo más importante de la paradoja de los gemelos es que nos parece muy real ya que en breve podremos realizar largos viajes y posiblemente a velocidades elevadas, con lo que la dilatación temporal se hará palpable.

Desde el punto de vista científico esta paradoja tiene otro aspecto importante, y es que pone en evidencia que los cálculos relativistas solo son sencillos cuando tenemos dos sistemas en movimiento relativo uniforme. 

Afortunadamente hemos visto que incluso en estos casos más complicados los diagramas de Minkowski muestran su gran potencia y nos permiten estudiar detalles que sin ellos quedarían muy oscuros.

Pero después de haber estudiado con bastante detalle la paradoja de los gemelos es fácil ver que detrás de ella hay mucho más.

A modo anecdótico vamos a comentar algunas situaciones que nos harán ver con más realismo los viajes interestelares (a grandes velocidades) y a distinguir los cálculos teóricos de la interpretación real. No podemos estudiar estas situaciones con demasiado detalle, así que las llamaremos “anécdotas”

Anécdota 1: siempre veremos las cosas de forma asimétrica.

Dijimos que una de las ideas fundamentales de la Relatividad es que no hay sistemas de referencia privilegiados. La consecuencia más importante es que si un sistema (la nave) se mueve respecto a otro (la Tierra), debe verse lo mismo que si el segundo sistema (la Tierra) se moviera respecto al primero (la nave).

Cuando usábamos como ejemplos dos trenes que se mueven uno respecto a otro la cosa estaba bastante clara, ya que sin referencias exteriores nadie sería capaz de decir si nos movemos o si es el otro tren el que se mueve respecto a nosotros.

El principio de relatividad de Einstein va más allá i afirma que “todos los sistemas inerciales son equivalentes”, por tanto la situación anterior debería ser totalmente simétrica. Si de la Tierra ven los relojes de la nave más lentos, desde la nave deberán ver los relojes de la Tierra más lentos.

Y es cierto.

Sin embargo ahora vamos a contradecirnos un poco y vamos a destacar aspectos asimétricos de los viajes como el de los gemelos.

En efecto, al estudiar el problema de los gemelos decíamos que la nave y la Tierra veían cosas simétricas y que la nave rompía la simetría al dar media vuelta y cambiar del sistema de referencia S’ al sistema S” para volver a la Tierra.

Si la situación fuese “totalmente simétrica”, debería tener sentido decir lo mismo de la Tierra: la Tierra debería poder romper la simetría dando media vuelta para volver a la nave.

Todos estaremos de acuerdo en que esto suena muy absurdo. Aunque el movimiento es relativo y las leyes de la física sean las mismas en la Tierra y en la nave, resulta difícil imaginar que la Tierra se está alejando de la nave y que vamos a frenarla y a hacerla volver hacia la nave.

En un texto o en un libro podemos cambiar las condiciones para aclarar mejor lo que queremos exponer, así hemos sugerido considerar dos trenes que se mueven en direcciones contrarias, pero en la realidad siempre un sistema (el S) será la Tierra o el sistema solar y el otro la nave o naves que se van y vuelven. ¿Habrá alguien capaz de imaginar que el sistema es simétrico cuando haga un viaje real? Evidentemente no. Siempre será la nave la que cambie de dirección y regrese a la Tierra y nunca al revés. Con esto estamos diciendo que, aunque en teoría no existen sistemas privilegiados,

Más aún, hemos repetido hasta la saciedad que un sistema debía tener un conjunto de observadores, y si llegamos a realizar viajes a las estrellas sin duda tendremos bases en muchos sistemas estelares, y estos materializarán el sistema de observadores de la Tierra, pero la nave nunca tendrá un sistema de observadores que pueda confirmar que el reloj de la Tierra retrasa respecto al de S’.

Posiblemente cuando se realicen viajes interestelares mucha gente estudiará R.E. pues interesará entender los pormenores de los viajes, pero nadie tomará en serio que no haya sistemas privilegiados.

Posiblemente hasta los pilotos de esas naves tendrán claro que hay sistemas privilegiados y todo el mundo lo aceptará así, cosa bastante normal pues al final todos bajarán de sus naves o volverán a la Tierra, y nunca será la Tierra la que “vuelva”.

Anécdota 2: Se usará el “tiempo vecino” como tiempo estándar.

Hemos dicho que incluso si la R.E. llega a formar parte de la cultura de mucha gente, probablemente nadie tomará en serio que no haya sistemas privilegiados.

Obsérvese que si esto es cierto resulta bastante razonable que las naves lleven un reloj con la hora de la Tierra (de S), igual que nosotros al ir al extranjero unos días seguimos considerando como hora buena la de nuestro país y sabemos que tendremos que volver a ella.

En cualquier momento podremos mirar este reloj (que irá más deprisa que el de la nave) para saber la hora de S, o sea la que consideraremos “hora verdadera” o tiempo estándar.

Ese tiempo se considerará más real que el tiempo biológico, igual que alguien que se hiberna no considera que su tiempo biológico detenido sea el tiempo real. Por otra parte toda nave llegará a su destino algún día y frenará, volviendo al sistema S, por lo que tiene interés saber la hora que será en S cuando paremos.

En cualquier viaje llevaremos un reloj con ese “tiempo de la Tierra”, pues será el tiempo más real para todos nosotros. Además será el tiempo patrón, al estilo de lo que hoy es en la Tierra el tiempo medio de Greenwich, y cualquier otro tiempo se comparará con este.

Por eso decíamos en el apartado anterior que cualquier viaje a velocidades lumínicas se experimentará como un salto al futuro, pues al volver a la Tierra encontraremos que ha pasado mucho más tiempo que para nosotros.

Anécdota 3: posiblemente se usarán medidas subjetivas aunque sean incorrectas.

No sería nada raro que se considerase como “velocidad real” el cociente del espacio recorrido en S dividido por el tiempo de la nave, ya que el espacio de S’ no aparecerá en los mapas que siempre estarán hechos en la Tierra. Así por ejemplo en nuestro viaje imaginario la nave podría considerar como “velocidad real” del viaje de ida los 4 años-luz recorridos (según los mapas, o sea según S) divididos por el tiempo de sus relojes, 3 años, resultando una velocidad superior a la de la luz que quizás ellos la consideren como velocidad real.

¿Cuál es el error? Que estamos tomando el espacio en S y el tiempo en S’, cosa claramente incorrecta, pero bastante razonable, pues esa será la sensación subjetiva para los viajeros.

Nosotros la llamaremos velocidad aparente pues tendrá una sensación muy real para los viajeros, pero también porque resulta ser muy usada en R.E. (bajo el nombre de cuadrivelocidad) para estudiar propiedades tan importantes como la energía y el momento (que nosotros no estudiaremos en este nivel introductorio)

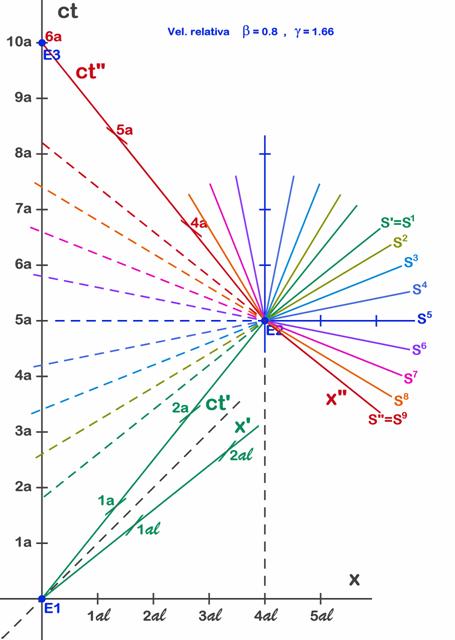
Anécdota 4: el problema de las aceleraciones.

Hasta ahora nos hemos centrado en un sólo sistema de referencia (por ejemplo S’) cada vez, relacionándolo con S. Pero ahora que ya entendemos un poco como funcionan, podemos revisar el significado de las aceleraciones en R.E.

Tradicionalmente se  ha dicho que en R.E. no se podía trabajar con sistemas acelerados, pero esto no es estrictamente cierto, ya que aunque resulte mucho más difícil que trabajar con sistemas inerciales (con velocidad constante), es una manera interesante de entender las dificultades propias de la R.G.

Aunque no haremos cálculos podemos entender la esencia de los sistemas acelerados con sólo mirar que ocurre en los diagramas de Minkowski durante la aceleración o el frenado del problema de los gemelos. Ésta es probablemente una de las maneras más sencillas de acercarse a la R.G.

En el problema de los gemelos hemos supuesto que la nave de Albert frenaba en un solo día, pasando de una velocidad de 0,8 c (0,8 veces la velocidad de la luz, o sea 240 000 km/s) a estar parado. Esto supone una aceleración inmensa (unos 280g, o sea unas 280 veces la fuerza de la gravedad terrestre), pero dado que esto simplificaba notablemente nuestros razonamientos decidimos suponer que algún día se superarán los problemas que generan estas aceleraciones tanto para las personas como para la estructura de la nave.

En las páginas anteriores hemos justificado que para el problema de los gemelos la clave no está el valor de la aceleración, sino el hecho de cambiar de un sistema S’ a otro S. Ahora volveremos sobre el diagrama de Minkowski para analizar lo que pasa durante este período de frenado, independientemente de que se realice en un día o en un año.

En los apartados anteriores hemos rehuido entrar en el problema y hemos simplificado el frenado hablando sólo del sistema inicial S’ y del sistema final S, pero en la realidad no podemos pasar directamente de la velocidad inicial (0,8 c) a la final (cero) sin pasar por todas las intermedias y esto significa que constantemente estamos cambiando de sistema de referencia pues cada velocidad por la que pasamos es un sistema de referencia distinto.

Como después acelerábamos de S a S” para el viaje de regreso, en la figura 7.9 estudiamos el cambio completo de S’ a S” como si no parásemos en la estación estelar. Precisamente hemos supuesto siempre estancias muy breves para poder despreciar esos tiempos.

El problema puede ser difícil hasta de imaginar pues cambiar de sistema de referencia significa, entre otras cosas, cambiar de conjunto de observadores. En la figura 7.9 hemos representado unos cuantos de estos sistemas (9 sistemas, en 9 colores distintos) que representan el proceso de transición de S’ a S” pasando por S (el sistema de la Tierra en azul).

Evidentemente estos sistemas representan los 6,4 años que habíamos perdido en el apartado anterior (ver Fig. 7.8 y comentarios en el texto). Sin embargo no hay que pensar que este tiempo pasa bruscamente para Albert, sino que hemos visto que es simplemente la diferencia entre lo que se ve desde S’y lo que se ve desde S” (lo que ven los observadores de S’ y lo que ven los de S”), pero lo que se ve (lo que ve Albert) no será real hasta que realice el viaje hasta la Tierra.

La manera de medir el tiempo de cada sistema no hace pasar el tiempo bruscamente, pero si que condiciona la manera de ver tu tiempo, por ejemplo tu futuro.

El hermano terrícola Tom no ha envejecido de golpe 6,4 años, sino que Albert ha cambiado de manera de ver el tiempo y “sabe” (porque no lo ve) que si sigue en este sistema verá este envejecimiento en su hermano al volver a casa (porque los cálculos se lo pronostican así). Sin embargo este envejecimiento no es real hasta que vuelve a la Tierra. Si el decidiera volver a cambiar de sistema antes de llegar a la Tierra podría cambiar el grado de envejecimiento, y si decide volver a alejarse de la Tierra podría volver a ver a su hermano más joven que él.

Fig. 7.9 -  Los 6,4 años que habíamos perdido se “ven” durante el proceso de aceleración,

pero sólo en potencia ya que sólo lo ve el conjunto (cambiante) de observadores.

En la Fig. 7.9 vemos 9 sistemas de referencia (en color continuo, a la derecha) por los que pasa Albert a lo largo del día de frenado y aceleración para volver a casa y a la izquierda vemos las líneas de lectura correspondientes (en línea de trazos) que muestran el tiempo que se ve en la Tierra desde cada uno de estos sistemas.

S¹ representa el eje de espacios verde o sea el del viaje de ida, por tanto en el que comienza a frenar. Prolongando el eje en sentido contrario (línea discontinua) vemos que ve en ese instante que el reloj de la Tierra marca 1,8 años.

Unas 6 horas después (S²) va a menor velocidad y mirando a la Tierra (prolongación del eje de S²) ve que ya han pasado 2,6 años.

Unas 6 horas después (S³) al mirar a la Tierra (prolongación del eje de S³) ve que ya han pasado 3,3 años.

Unas 6 horas después (S⁴) mira a la Tierra (prolongación del eje de S⁴) y ve que ya han pasado 4,2 años.

Al terminar el primer día (S⁵) se encuentra en S, o sea que se ha parado en el sistema de la base estelar, que es el mismo de la Tierra. Mirando a la Tierra (prolongación del eje de S⁵) ve que ya han pasado 5 años.

Realmente cuando decimos que mira a la Tierra sabemos que es una forma de hablar. Albert sólo puede hacer los cálculos, pero no puede ver cosas que ocurren tan lejos. No puede ver la Tierra ni puede ver a sus observadores. La información de estos no puede ir más rápida que la luz y por tanto desde la Tierra tardaría años en llegarle.

Al terminar su breve estancia en la base estelar, comienza la aceleración para regresar a la Tierra (realmente frenado y aceleración posterior son aceleraciones del mismo sentido).

Durante este proceso pasa por los sistemas S6, S7 y S8 para llegar finalmente a S9, que es el sistema S” rojo en el que vuelve a la Tierra. Cada sistema corresponde a una velocidad de la nave (0; 0,2; 0,4; 0,6 y 0,8 veces la velocidad de la luz) y cada cambio de sistema (cambia constantemente, no permanece en ninguno de los intermedios) representa que cambia el conjunto de observadores en los que confía. Luego realmente durante la aceleración es como si no tuviera observadores, pues no tiene tiempo para recibir información de ellos.

Insistimos en que lo que decimos que “ha visto” sólo lo ha visto en potencia, sólo lo ha calculado. Por tanto no ha visto envejecer 6,4 años a su hermano. Lo único cierto y objetivo es que para él sólo ha pasado 1 día.

Insistimos en que esos 6,4 años realmente no han transcurrido, aunque sus nuevos observadores le dicen que sí. ¿Porqué decimos entonces que no han transcurrido? Porque sólo serán reales si continuamos con el viaje de vuelta, pero podríamos decidir volver a cambiar de sistema y cambiar de escalas de tiempo de nuevo.

Si aceptamos que podemos cambiar de sistema en cualquier momento, si podemos acelerar no tiene sentido decir que algo ha pasado ya en la Tierra (una fecha determinada nuestra) porque podemos cambiar a otro sistema en el que aun no haya pasado.

Si aceptamos aceleraciones todas nuestras escalas temporales lo son sólo en potencia y ningún hecho alejado es un hecho consumado hasta que nos llega la información. El problema reside en que en un sistema acelerado la simultaneidad es relativa, como veíamos en el problema del garaje.

Esto genera el problema de que no tengamos una escala de tiempos fiable para intercambiar información con los demás y en consecuencia:

El problema es importante y es el mismo problema que tendremos en la R.G.: no podemos sincronizar nuestros relojes con los de la Tierra (que era el tiempo estandar) y por tanto en la nave no pueden hablar del tiempo de la Tierra. No pueden saber si ha pasado un día determinado o no, y eso no porque no lo sepan, sino porque no tiene sentido la pregunta pues a cada instante cambia su escala de tiempos.

Anécdota 5: la flecha del tiempo y la secuencia de información.

Tal como nos pasó al estudiar la inversión temporal, puede parecer que estamos diciendo que podemos cambiar a otro sistema y usarlo para ir al pasado, pero no es así. Dijimos allí que en R.E. el tiempo tiene una dirección bien definida (véase el cono de luz, Fig. 6.11). Debido a que tiene una dirección se habla de la flecha del tiempo.

Es una situación similar a la de la inversión temporal. Cosas que sucedían en lugares distintos se podían ver en un orden desde S y en el orden inverso en otro sistema S’. Ahora durante un día de frenado Albert calcula que su hermano habrá envejecido 6,4 años, sin embargo eso no ha ocurrido de manera irrevocable, pues podemos cambiar a otro sistema en el que aun no se vea como hecho.

Si podemos acelerar podemos cambiar de sistema cuando queramos.

Sin embargo no podemos hacer lo que queramos con el tiempo, pues una cosa que ya haya ocurrido y hayamos visto no se puede volver atrás. Si Tom envía mensajes diarios a Albert y este recibe una foto de cuando el niño tenía 2 años, por más que cambie de sistema jamás podrá volver a un pasado anterior a los dos años del niño.

¿Y si no le envía la foto? Evidentemente tampoco. No depende de lo que le envíe, sino de si la información tiene tiempo de llegar.

Cuando Albert llega a la estrella y pide los últimos mensajes de su hermano le darán mensajes de 4 años antes ya que todos los mensajes llegan con 4 años de retraso debido a la distancia (4 al) que les separa de la Tierra.

Pero como Albert lleva 5 años de viaje (visto desde S) verá los mensajes hasta el primer año después de su partida. La foto más reciente de su sobrino será la de cuando cumplió 1 año, aunque por el reloj de la estación estelar “sabe” que el niño ya debe tener 5 años.

¿Lo sabe de verdad?

¡No! El niño tiene 5 años en potencia, pero si cambia de sistema otra vez (y lo hace, pues al día siguiente inicia su viaje de regreso a la Tierra) esa edad cambia para Albert. La simultaneidad depende del sistema en el que estemos.

Sin embargo no podrá cambiar el hecho de que ya ha recibido la foto del primer cumpleaños de su sobrino. Y todos los hechos que han ocurrido dentro del primer año de viaje (y de su sobrino) también pertenecen a su pasado, tanto si los que le han comunicado como los que no.

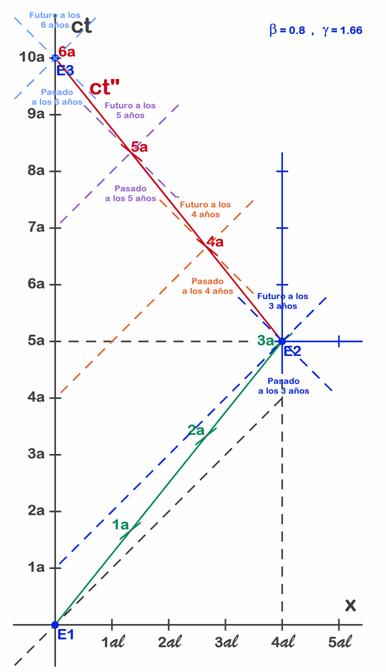
En la figura 7.10 hemos dibujado la línea de luz azul (discontinua a trazos azul) correspondiente a la llegada a la estrella. Aunque parece una línea de lectura, no lo es, ya que no es paralela a los ejes, sino que es la bisectriz, que sabemos que representa el viaje de un pulso de luz porque corresponde a una velocidad de un año-luz cada año, y esto es lo que recorre la luz, y ningún objeto material puede alcanzarla.

Tal como vimos en el apartado A.6.8 esas líneas de 45 grados separan el pasado (zona por debajo del suceso) y el futuro (zona por encima del suceso). Este esquema se utiliza también en relatividad general y recibe el nombre de cono de luz, ya que la velocidad de la luz (la bisectriz de 45º) determina la información que puedes haber recibido y la que no.

Fig. 7.10 -  El cono de luz determina a cada instante lo que pertenece a tu pasado y lo
que pertenece a tu futuro. Lo que cae fuera de él “depende” del sistema de referencia.

Vemos en la figura 7.10 que el primer año de la Tierra cae dentro del cono inferior azul, o sea dentro del pasado de Albert para ese momento. El momento en que llega a la estrella está señalado en el gráfico como E2, o como año tercero de su viaje (3a).

Igualmente podemos dibujar el cono de luz para cualquier otro momento del viaje y sabremos lo que pertenece al pasado de Albert como hecho consumado. Lo que queda fuera del cono, es decir, lo que queda a derecha e izquierda, se puede ver como pasado o como futuro dependiendo del sistema de referencia desde el que miremos.

Así por ejemplo hemos trazado en naranja las líneas de 45º para el cuarto año de viaje (4a) y nos dicen que en ese momento Albert habrá recibido la información del cuarto año de la Tierra. Los cuatro primeros años de su sobrino ya pertenecen a su pasado, y por más que cambie de sistema no puede conseguir escapar al hecho de que esa información, esa luz, ya le ha alcanzado. Él no puede alejarse más allá de esa luz porque no puede superar la velocidad de la luz.

Observamos que a los tres años, cuando llegó a la estrella decíamos que el niño había cumplido 5 años, pero como aun no caía dentro de su cono de pasado, eso era “opinable”.

Vemos que esa fecha (5a para la Tierra) todavía no cae dentro del cono del pasado naranja, por tanto aun puede cambiar de sistema y hacer que eso pertenezca a su futuro (a pesar de que hace 1 año que ya pertenecía a su pasado). La manera de hacerlo es volver a cambiar de dirección y alejarse de la Tierra. A la velocidad adecuada ese hecho (los cinco años del niño) puede verse como un hecho futuro.

Las bisectrices violetas marcan el cono de luz del quinto año de viaje (5a  rojo), para el cual vemos que Albert ve como pasado hasta el año 7 de la Tierra (7a negro).

Y finalmente al llegar a la Tierra ve como pasado los 10 años de la Tierra (cono de luz azul celeste de los 6a rojos).

Para hacernos una imagen clara de la situación conviene suponer que todo lo que pasa en la Tierra se retransmite a través de ondas electromagnéticas (radio, tv, ...), de manera que la información recibida pasa a pertenecer a su pasado. La información no recibida se puede imaginar viajando por el espacio a la extraordinaria velocidad de 300 000 km/h, que aunque muy rápida para escalas humanas no resulta tan rápida a escalas astronómicas como las que estamos manejando.

Si “no queremos recibir una información” nos basta alejarnos de ella a gran velocidad. No conseguiremos retrasarla para siempre, pues la luz viaja a la mayor velocidad posible del universo, pero posiblemente podemos retrasarla mucho tiempo.

Para cerrar esta reflexión sobre la flecha del tiempo y el cono de luz, podemos observar que durante el viaje de ida, dado que nos alejábamos de la Tierra, también nos alejábamos de la información que esta nos enviaba, e íbamos retrasando ese pasado. Observámos que en tres años de viaje sólo hemos recibido un año de información de la Tierra. Sólo hay un año de la Tierra que pertenezca a nuestro “pasado seguro” o pasado de hecho.

Sin embargo durante el viaje de vuelta por cada año de nuestro viaje recibimos información de tres años de la Tierra. Esto es debido a que corremos en dirección hacia la Tierra y por tanto en dirección hacia los mensajes que esta nos envía.

Podríamos decir que durante el viaje de vuelta nos vemos bombardeados por una cantidad inmensa de información, toda aquella información de la que nos habíamos alejado durante el viaje de ida más la generada durante la vuelta.

Es en esta recepción acelerada de información es donde realmente se recuperan los 6,4 años que habíamos perdido (apartado A.7.8 y Fig. 7.8) al cambiar de sentido en la estrella (E2) y no durante el tiempo de aceleración.

A medida que Albert va recibiendo esa información ve crecer a su sobrino y ve envejecer a su hermano. Ambos procesos ahora se ven de verdad y es cuando se vuelven reales, ya que después de verlos ya no podemos cambiar de sistema para cambiar ese pasado.

Anécdota 6: las dificultades de los sistemas de referencia acelerados.

Al comentar la Fig. 7.9 hemos dicho que los sistemas de referencia acelerados resultan complicados, pero no estamos diciendo que no se puedan considerar. De hecho, haciendo un pequeño esfuerzo de imaginación, puede resultar una extraordinaria introducción a la R.G.

¿Cual es la dificultad?

Para materializar el sistema de observadores de S’ habíamos imaginado un tren de naves que iba sin parar de en la dirección de la Tierra a la Estrella. Supongamos, para fijar ideas, que el tren tiene exactamente la misma longitud que distancia separa la Tierra (T) de la estrella (E). Esto significa que cuando Albert (A) llega a la estrella (Fig. 7.12), el observador de cola (B) pasa exactamente al lado de la Tierra. Este es el observador que le informa de que en la Tierra sólo han pasado 1,8 años (ver Fig. 7.6 o 7.8).

Imaginemos ahora que todo el tren es una sola nave, un cuerpo sólido de una sola pieza. Este hecho plantea problemas, pero puede ayudarnos a concebir la idea de simultaneidad en un entorno (movimiento acelerado) donde hemos dicho que este era un concepto difícil.

Fig. 7.11 -  Para concretar el sistema de referencia de Albert imaginamos un “tren de naves”
muy largo, de manera que siempre tengamos un observador de S’ (un vagón) junto a la Tierra.

En la figura 7.11 podemos ver un detalle importante: cuando Albert sale de la Tierra la nave ya era tan extensa como al final y el observador de cola ya existía e iba a la misma velocidad y en la misma dirección que Albert.

Fig. 7.12 -  Podemos imaginar un “tren de naves” tan largo que cuando Albert (A) 

llega a la estrella (E), el observador de cola (B) se encuentre junto a la Tierra (T).

La dificultad de la situación consiste en intentar imaginar que ocurre cuando frenamos una nave de estas dimensiones. Si eso tiene sentido quizás podríamos introducir el concepto de sistema de referencia acelerado, pero veremos que existen dificultades importantes, como el hecho de no poder sincronizar los relojes.

Podemos ver en la figura 7.9 que cuando comenzamos a frenar (aceleración negativa), los relojes de la punta de la nave (donde está Albert) van más despacio que los de la cola (donde va el observador B).

Ahora las barras de colores no representan un nuevo sistema de observadores, sino un mismo conjunto de observadores (aunque quizás no deberíamos llamarles así) que se encuentran físicamente dentro de una extensísima nave.

Supondremos para simplificar que Albert no se detiene en la estrella, sino que frena y acelera en sentido contrario en dos dias. Lo que primero que nos llama la atención es una diferencia muy exagerada en la marcha de los relojes de Albert en la punta y el observador (B) en la cola:

La situación parece complicada, pues la diferencia de tiempos resulta muy exagerada. No es un pequeño retraso como ocurría entre S y S’, así que sincronizar relojes parece que será difícil.

Conviene aclarar que una nave tan larga no daría la vuelta pues la cola está muy cerca de casa y darle la vuelta sería hacerle realizar un viaje de otros 10 años (hasta E2) innecesariamente. El proceso es el mismo que suelen seguir muchos trenes: primero frenar y después iniciar la marcha en sentido contrario sin girar.

Estudiar la situación con detalle es complicado, así que sólo daremos una mirada superficial para comprobar si es posible establecer un sistema de referencia dentro de una nave acelerada.

En R.G. se añade la complejidad adicional de que los diferentes vagones del tren están con frecuencia sometidos a aceleraciones distintas (en realidad a distintas fuerzas gravitatorias), de manera que la sincronización resulta francamente complicada. Veremos que aquí no es muy diferente.

¿Como elegimos un tiempo estándar?

Dado que durante la aceleración los tiempos siguen ritmos distintos en cada punto de la nave, aunque comenzasen sincronizados (que así era cuando eran observadores de S’), al cabo de un instante de aceleración todos los relojes ya irán desfasados. Cuanto más cerca de la punta, más lentos van los relojes, y cuanto más cerca de la cola, más adelantan.

Cuando hablábamos del tiempo vecino (anécdota 2) dijimos que el tiempo de la Tierra (tiempo vecino) sería el mejor candidato a tiempo estándar. Ahora la situación es similar y debemos elegir un tiempo estándar y colocar a lo largo de la nave relojes sincronizados con ese tiempo estándar. Si somos capaces de calcular el ritmo al que va el reloj del otro extremo de la nave, podremos crear un reloj que vaya a ese ritmo, por tanto si queremos sincronizarnos sólo hay que decidir una manera y respetar la norma adoptada. El tiempo estándar podría ser también el de la Tierra, pues su única finalidad es permitir la sincronización entre los diferentes puntos de la nave.

Una vez elegido ese tiempo estándar, para verificar periódicamente el buen funcionamiento del sistema podemos emitir un patrón de radio que se pueda recibir en todas partes y que se utilice para sincronizar los relojes. De hecho en el mundo real lo hacemos así y los relojes atómicos más importantes y precisos del mundo emiten señales para que los demás podamos sincronizarnos con una elevada precisión.

Dado que no podemos extendernos más sobre este tema, terminaremos con unas observaciones sobre algunas de las dificultades adicionales que nos encontraremos al intentar utilizar sistemas acelerados como este:

- Toda la nave puede ir a la misma velocidad y estar en un mismo sistema a lo largo de todo el movimiento acelerado y sin embargo el tiempo es distinto para cada punto de la nave.

- Es difícil incluso determinar donde estará cada punto de la nave, pues además de moverse cambia de longitud al cambiar de velocidad (cambia su contracción longitudinal).

- Los habitantes de la nave, ayudados de un reloj estándar, se pueden intentar utilizar como observadores del sistema acelerado (habría que redefinir lo que entendemos por observador), pero no servirían como observadores de los sistemas por los que pasamos (sistema asociado a una velocidad instantánea) pues no tienen relojes sincronizados para esos sistemas.