A.7. La paradoja de los gemelos, 3^a parte.

A.7.7.  Asimetría del problema de los gemelos: importancia del tiempo vecino.

Sobre el diagrama las conclusiones son claras (igual que si hubiéramos hecho los cálculos), pero sorprende que la simetría de las ecuaciones de Lorentz no lleve a una situación final simétrica.

Uno tiende a fijarse en los dos trayectos por separado (de hecho hemos estudiado los dos trayectos por separado) y sabemos que cada uno de ellos es perfectamente simétrico.

Sin embargo al combinar ambos viajes el resultado final no es simétrico. Tom, quedando en la Tierra envejece mucho más que Albert. ¿Porqué no es simétrico el resultado final?

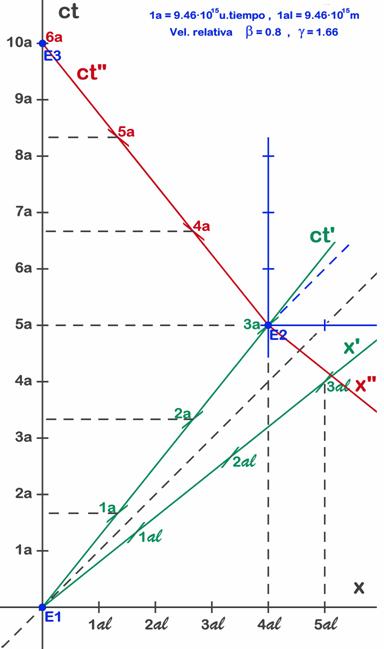
Como primera aproximación al problema revisaremos la simetría del viaje de ida, pues la mayoría de libros se quedan con la idea superficial de que cada uno “ve como el reloj del otro va más despacio”, pero esto no es todo, ni siquiera es el dato más importante para entender este problema.

En nuestro modelo suponíamos que había observadores en todas partes, y esto significa que durante todo su viaje de ida Albert se ha ido encontrando observadores de S a su lado que le dicen que en la Tierra ha pasado más tiempo que el que marca su propio reloj.

Así por ejemplo cuando su reloj marca 1 año, el de los observadores de S que están a su lado marca 1,66 años y cuando el suyo marca 2 años, ve que el reloj de los observadores de S que están a su lado marca 3,33 años y le aseguran que en la Tierra ha pasado ese tiempo.

¿Como se lee la hora del observador de S en el diagrama? Pues lógicamente trazando una horizontal (paralela al eje negro) desde el punto en el que se encuentra el astronauta, pues el observador citado está en S, que es el sistema de líneas negras (ver Fig. 7.7).

Sin embargo los observadores de S’, aquellos de los que se fía Albert (porque con ellos las cosas cuadran bien), le dicen que en la Tierra ha pasado menos tiempo sólo 1,2 años (Fig. 7.6).

Así pues, desde S’ ven los relojes de sus vecinos de S mal sincronizados.

Si nos ponemos por un momento en la piel de Albert y repasamos todo lo visto resulta que  una de las características de los viajes relativistas es que la dilatación de tiempos se ve sobre el reloj de S del que nos alejamos (en nuestros ejemplos el reloj de Tom en la Tierra), pero no en los relojes de S que vemos junto a nosotros.

Si miramos el reloj del observador que tenemos a nuestro lado (Fig. 7.7), su tiempo se ve correr más rápido. El tiempo que Albert ve en el reloj de S que tiene a su lado en cada momento es un tiempo observado en relojes distintos a cada momento, es un tiempo que no corre en ningún reloj, pero es el tiempo importante, ya que es el que encontrará si se para allí (como hace en la estación estelar), y este tiempo va más deprisa que el suyo, como se ve en la figura 7.7

Fig. 7.7 -  Durante la ida Albert ve en los relojes vecinos (de S) un tiempo vecino de 1,66 años,

2,33 años y 5 años. A la vuelta ve un tiempo vecino de 6,66 años, 8,33 años y 10 años.

En esta figura hemos dibujado las líneas de lectura que nos permiten ver ese tiempo, el del observador de S que tenemos a nuestro lado mientras viajamos. Llamaremos “tiempo vecino” a este tiempo que lee Albert en el reloj de S que ve a su lado, y llamaremos ”relojes vecinos” a esos relojes porque en cada instante sólo miramos el que tenemos al lado (Fig. 7.7).

Insistimos en que no es el tiempo de ningún reloj concreto, sino que consiste en leer un reloj distinto en cada momento, el reloj de S que pasa por su lado en cada instante. Todos los observadores de S’ ven cosas similares a Albert, es decir, ven los relojes de S desincronizados, pero no de cualquier manera, sino que los relojes más próximos a la Tierra marcan tiempos muy atrasados, pero los que están más allá de Albert marcan tiempos muy adelantados (aunque cada reloj individual de S se ve más lento que el reloj de Albert).

Si no piensas pararte el tiempo vecino no tiene gran importancia (y lo ven igual ambos sistemas), pero si te paras adoptas ese tiempo como el tuyo propio, así que ahí está la gran diferencia entre ambos gemelos. Lo que hace asimétrico el problema es el hecho de parar, o más genéricamente, el hecho de que Albert cambia de sistema de referencia al cambiar del tren a la estación estelar o al tren de vuelta. En ese momento, al parar, adopta el tiempo de S y abandona el de S’.

Muchos autores dan importancia a la aceleración de frenado, pero es un mal enfoque del problema, ya que da la sensación de que es el valor de la aceleración lo que importa, y no es así. Lo que importa es cambiar de sistema, ya que adoptamos el tiempo del sistema en el que entramos, y hemos visto que el tiempo vecino siempre va más rápido.

La asimetría reside precisamente en que Tom, en la Tierra, nunca cambia de sistema, nunca adopta el tiempo de S’ (que como todo tiempo vecino va más rápido).

Albert ve el tiempo vecino ir más rápido durante el viaje de ida (Fig. 7.7) y también durante el viaje de vuelta, de forma que al llegar a la Tierra ha visto acumularse muchísimo “tiempo vecino” en los relojes vecinos (10 años, o sea 4 más que en su reloj) y por tanto en todo momento “ve” claramente que fuera de su nave el tiempo pasa más rápido y en todo momento tiene claro que al regresar a la Tierra encontrará a su hermano más viejo. (En el próximo apartado discutiremos más a fondo esta idea de que “ve” pasar más rápido el tiempo de fuera de la nave, ya que en primera impresión puede parecer una idea que contradice la dilatación temporal).

Aunque Albert ve como los relojes de S van más lentos (por ejemplo el de Tom que permanece en la Tierra), eso no es lo importante, ya que Tom nunca subirá al tren de Albert y por tanto nunca asumirá ese tiempo (menor) como suyo. Por el contrario Albert si cambiará de sistema y volverá a S.  Luego la situación no es tan simétrica como habíamos supuesto. La intención de Albert de cambiar hace que su tiempo vecino sea el importante.

En un viaje real la situación no es nada simétrica, pues desde el principio Albert tiene intención de parar y volver atrás, por lo que mirará el tiempo vecino como un tiempo real, mientras que Tom en ningún momento se ha planteado “parar” y “regresar” hacia Albert.

Tom nunca cambia de sistema y eso hace que su tiempo sea el “real”, el que se toma como patrón. Eso hace asimétrica la situación.

Así pues estamos afirmando que cada viaje (ida y vuelta) por separado es perfectamente simétrico, pero globalmente hay una clara asimetría que da al tiempo de T un peso que el de A no tiene (también analizaremos esto en los apartados siguientes).

Para Tom el tiempo vecino es una falacia. En un viaje real ni siquiera es visible, pues el tren de naves no es factible y Tom nunca verá tal tiempo vecino. Pero aun si existiera, el hecho de que no tenga intención de “parar” y subirse a ese tren hace que no tenga importancia para él, mientras que para Albert sí es importante pues para en la estrella y asume el tiempo vecino como tiempo propio.

En los dos apartados siguientes revisaremos los puntos más relevantes de la paradoja de los gemelos. En el primero sacaremos conclusiones con la intención de entenderla mejor y en el segundo comentaremos algunos aspectos que sugieren la necesidad de una teoría más amplia, la Relatividad General.

A.7.8.  Conclusiones importantes sobre la paradoja de los gemelos:

El viaje de ida es simétrico para Albert y Tom, pues el movimiento relativo de uno y otro es el mismo y cada uno ve el tiempo del otro más lento.

Sin embargo cuando el gemelo astronauta decide frenar y volver al sistema S parando en la base estelar E2 el problema deja de ser simétrico, al menos durante el proceso de frenado. Lo más relevante para entender la diferencia es que Tom no cambia de sistema, pues no cambia de velocidad, mientras que Albert cambia de sistema (de S’ a S de la estación estelar y después a S” durante el viaje de vuelta).

Está claro que parar y regresar al punto de partida representa una asimetría importante. Sin embargo la aceleración (la intensidad del a frenada) no la tiene. Dediquemos un momento a ver porqué no la tiene.

Sobre el diagrama de Minkowski parece claro que si cambiamos de S’ a S” en un día la aceleración será aproximadamente doble de si cambiamos de S’ a S” en dos días, pero la única diferencia entre los dos casos será haber perdido un día más (despreciable dado lo largo del viaje). Por lo demás todo será exactamente igual, por tanto el valor de la aceleración parece no tener demasiada importancia.

Para verlo más claro podemos imaginar que Albert tenga libertad suficiente como para poder decidir si regresa o no a la Tierra. Supongamos entonces que después de pasar un día en la estación estelar decide no volver a la Tierra y opta por continuar su aventura e ir más lejos. ¿Que ocurre si vuelve a subir al tren que se aleja de la Tierra?

Al comenzar con la paradoja de los gemelos suponíamos que se hubiera descubierto alguna tecnología que permitiera a los astronautas sobrevivir a grandes aceleraciones. Supongamos entonces que acelerara de nuevo en un solo día en dirección del tren S’ que se aleja de la Tierra. En principio cogería el tren un par de vagones más atrás, pero su tiempo sólo diferiría en un día o dos del que vería si no hubiera bajado del tren. Tom desde la Tierra vería algo similar.

Entonces, aunque Albert se habría sometido dos veces a grandes aceleraciones (frenada y aceleración), estas apenas afectarían a su tiempo. Él vería para la Tierra lo mismo que si no hubiera parado nunca, y su hermano Tom desde la Tierra vería a Albert igual que si no hubiera parado en la estación estelar.

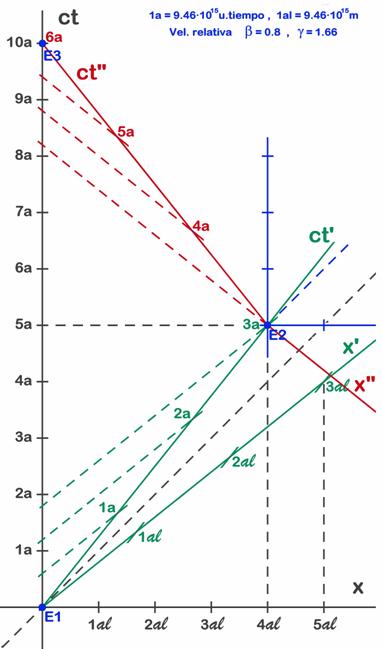
¿Entonces porqué se da tanta importancia a la aceleración?

Realmente durante el período de aceleración ocurre una cosa curiosa que mal analizada da pie a pensar que lo importante es la aceleración. En la figura 7.8, que es una reproducción de la 7.6, vemos que al cambiar del sistema S’ verde al S” rojo parece producirse un salto brusco de 6,4 años, pues en un instante (realmente en los dos o tres días que tarda en pasar de uno a otro) la escala de tiempos de Albert cambia bruscamente de ver 1,8 años en el reloj de la Tierra (tercera línea de lectura verde) a ver 8,2 años en el instante siguiente (primera línea de lectura roja).

Da la sensación de que se volatilizan 6,4 años de la vida de Tom, pues Albert ve como el reloj de la Tierra salta bruscamente 6,4 años. Pero como ya hemos dicho en otras ocasiones, estas situaciones paradójicas dejan de serlo cuando se analizan a fondo.

¿Qué ocurre durante el tiempo de frenada y aceleración?

Si delimitamos un poco más la paradoja veremos que por más que sea muy llamativa, es sólo una fantasía, y a la vez esto nos ayudará a entender más a fondo la estructura de los sistemas de referencia (y sus conjuntos de observadores).

Durante el viaje de ida de 3 años Albert sólo ve pasar 1,8 años de la vida de Tom, los cuales son los primeros 1,8 años del viaje para Tom. Queremos insistir en el significado de esto porque no es una situación de laboratorio, sino una situación muy real. Si llegamos a hacer viajes a estas velocidades será exactamente lo que pasará.

Para hacernos una idea más concreta de lo que decimos, supongamos que el día antes de iniciarse el viaje de Albert, Tom tuviera un hijo. Entonces lo que decimos es que Albert, durante sus tres años de viaje de ida parece ver los primeros 1,8 años de vida de ese niño.

Si miramos el viaje de vuelta vemos que también ve 1,8 años de la vida de Tom, y por tanto también de su hijo. Pero ahora son los últimos 1,8 años, o sea desde que el niño tiene 8,2 años hasta que cumple los 10 años (cuando su tío Albert llega de vuelta a la Tierra).

Albert llega a la Tierra cuando para ésta han pasado 10 años, pero sólo ha visto 1,8 durante la ida y otros 1,8 durante la vuelta, Esto hace 3,6 años. ¿Dónde están los 6,4 años restantes? ¿Se ha perdido de los 1,8 a los 8,2 años de su sobrino?

Evidentemente estos años no se han volatilizado, y la paradoja reside en que sobre el diagrama parece que transcurren durante los 2 o 3 días que Albert pasa junto a la estrella, y lógicamente mucha gente asocia este paso “acelerado” del tiempo con el proceso de frenado y aceleración de Albert, pero no es así.

Fig. 7.8 -  Durante la ida está en el sistema S’ verde y ve pasar 1,8 años en

el reloj de la Tierra. Durante la vuelta está en S” rojo y ve pasar otros 1,8

años (de 8,2 a 10 años) en la Tierra ¿Donde están los 6,4 años restantes?.

El hecho es que Albert no ve 1,8 años durante la ida ni 1,8 años durante la vuelta. Es el sistema S’ el que ve 1,8 años del viaje de ida y el sistema S” el que ve los 1,8 del viaje de vuelta. Albert lo único que hace es confiar en los observadores de su sistema, pero las cosas ocurren demasiado lejos como para que se pueda decir que “ve” pasar el tiempo en la Tierra. Ni siquiera tiene tiempo de recibir “informes” de sus observadores junto a la Tierra, ya que esos observadores están tan lejos que sus “informes tardarán años en llegar hasta Albert... por tanto en la realidad Albert ve muy poca cosa.

En nuestra vida cotidiana las distancias entre lo que ocurre a nuestro alrededor y nosotros son muy cortas comparadas con la velocidad de la luz. Estamos acostumbrados a ver todo lo que ocurre a nuestro alrededor de forma instantánea, pues para distancias cortas la imagen parece llegar enseguida a nuestra retina.

Sin embargo cuando las distancias se vuelven grandes la información deja de ser instantánea, y en cierta manera pasamos a sufrir “ceguera cosmológica”, pues nunca vemos las cosas cuando ocurren, sino mucho más tarde (en nuestro ejemplo años más tarde).

En cambio el sistema de referencia, el conjunto de observadores, si que ve las cosas instantáneamente, aunque sólo a través de un observador: el que está junto al suceso.

¿Entonces donde están esos 6,4 años? ¿Transcurren durante el periodo de aceleración o no?

Naturalmente no transcurren durante el tiempo de aceleración.

Las dos claves para entender lo que ocurre son el concepto de tiempo vecino (ver A.7.7) y el concepto de sistema de referencia como conjunto de observadores (ver cuadro anterior).

Albert, durante su viaje de ida, no ve los 1,8 años de la Tierra que se calculan sobre el diagrama de Minkowski. Esto es lo que ve el sistema S’, o sea su conjunto de observadores. Pero en cuanto el decide frenar y cambiar al sistema S de la estrella, esos que eran sus observadores dejan de serlo. Deja de confiar en los de S’ y vuelve a confiar en los de S.

El tiempo vecino es importante porque es el que permite entender lo que ve Albert, que es lo importante en una situación como esta. El tiempo importante en cuanto se detiene en la Estrella es el tiempo del observador (de S) que tenía a su lado, o sea el tiempo vecino. Lo que dice un observador que está junto a la Tierra no tiene ninguna importancia, especialmente si pensamos abandonar ese sistema (S’). Albert abandona S’ mucho antes de poder recibir noticias de ese observador, por tanto la información de lo que ve ese sistema de observadores no tiene ningún interés (llegará con años de retraso) para Albert.

En R.E. el tiempo de tus observadores tiene mucha importancia si no piensas cambiar de sistema. Ésta es una limitación importante de la teoría: sólo permite hablar de simultaneidad si los sistemas que comparamos van a velocidad constante, es decir, si ambos son sistemas inerciales.

En el momento en que tu velocidad cambia, en el momento en que aparecen aceleraciones (una frenada es una aceleración negativa) ya no hay cálculos sencillos y, mucho más importante, ya no hay un concepto sencillo de simultaneidad.

En el apartado siguiente discutiremos un poco más los problemas de los movimientos acelerados, y los interpretaremos (Fig. 7.9) como un cambio constante de sistema de observadores. En particular veremos que en un sistema acelerado no podemos mantener un conjunto de observadores porque el hipotético sistema de referencia se movería a velocidades diferentes en cada punto y en puntos alejados (por tanto los observadores alejados) debería ir a velocidades superiores a la de la luz. 

Al no haber un concepto sencillo de simultaneidad resulta difícil contestar a la pregunta que nos hemos hecho ¿Entonces donde están esos 6,4 años? ¿Transcurren durante el periodo de aceleración o no?

La respuesta correcta sería “depende del observador”, pero esto es tanto como no responder y no nos ayuda a entender lo que ocurre.

En realidad, como veremos en el próximo apartado, cuando yo acelero (por ejemplo al partir de la estrella hacia la Tierra) cambio de observadores, y estos “me dicen” que los relojes de S se están adelantando. Cuanto más lejos de mí, más se adelantan los relojes de S.

¿Es un cambio real?

Evidentemente no. Podríamos decir que es un cambio potencial, en el sentido de que sólo se hará real si continúo en ese sistema durante unos años más.

Pero ya hemos dicho que si al cabo de un día más decido volver al antiguo sistema S’ (es decir, si vuelvo a alejarme de la Tierra), nada de eso llegará a ser real. Resultará evidente que fue un espejismo momentáneo.

Para ver claramente el espejismo (debido al cambio de simultaneidad) volvamos a pensar en el sobrino de Albert y hagámoslo en primera persona, como si nosotros fuéramos Albert o viajásemos en la misma nave que él.

Durante el viaje, antes de llegar a la estrella hemos visto 1,8 años de la vida del niño (nuestros observadores de S’, no nosotros), pero por el hecho de frenar pasamos a S, donde (los observadores de S) han visto 5 años de la vida del niño. Si ahora encendemos motores para regresar pasamos a S”, donde (los nuevos observadores de S”) han visto 8,2 años de la vida del niño.

¿Donde está el espejismo?

En que todos estos cambios se han visto en tres días, y podemos deshacerlos en otros tantos días con sólo cambiar de opinión y deshacer lo hecho. Si volvemos a frenar, y por tanto volvemos a S, volveremos a ver sólo 5 años de la Tierra, y si volvemos al sistema S’ para seguir alejándonos de la Tierra, volveremos a ver sólo 1,8 años de la Tierra o del sobrino de Albert.

Si esto fuera lo que parece, con estas triquiñuelas podríamos ver el futuro del niño (cuando nos incorporamos al sistema S”) y volver a su pasado (al volver a S’), pero desgraciadamente es sólo un espejismo, un juego de palabras.

El sistema S’ mira la simultaneidad de una manera, y el S” de otra muy distinta, de forma que lo que para uno es pasado, para el otro es el futuro, pero como decíamos en la página anterior, es el sistema, considerado como conjunto de observadores, el que ve eso, pero no lo ve Albert.

Por el hecho de cambiar de sistema de referencia no ves cosas alejadas, simplemente cambia la forma de medir el tiempo y la simultaneidad. Pero el cambio sólo es “en potencia”, no llegará a ser un cambio “de hecho” a menos que continúes en ese sistema el tiempo suficiente.

En resumen, las cosas que suceden muy lejos (aquí la vida del niño entre los 2 y los 8 años) puede que no sucedan ni en tu presente, ni en tu pasado ni en tu futuro, sino que puedas elegir cualquiera de los tres casos con sólo cambiar de sistema de referencia.

Esto es lo que significa que en R.E. la simultaneidad es relativa.

Respondiendo pues a la pregunta que nos hacíamos al principio, podemos afirmar que esos 6,4 años no se ven pasar durante el tiempo de aceleración de Albert.

Podríamos pensar que “el sistema de referencia de Albert ve pasar esos 6,4 años durante esos tres dias”, pero eso tampoco es correcto, ya que no existe un sistema de referencia durante el tiempo de aceleración. En el próximo apartado veremos (Fig. 7.9) que el tiempo de aceleración cambiamos constantemente de sistema, es decir, a cada instante dejamos de confiar en nuestros observadores anteriores para pasar a apoyarnos en un nuevo conjunto de observadores.

Podemos terminar este apartado resumiendo como funciona el tiempo durante el frenado y aceleración de la nave, ya que es la parte más interesante de todo lo que hemos visto de la paradoja de los gemelos.

Durante el viaje de ida hemos encontrado “vecinos” de S que llevaban su reloj adelantado. Es decir, cada reloj de S va más despacio que el nuestro, pero como los relojes más alejados van más adelantados, el tiempo de nuestro vecino siempre es mayor que el nuestro, el tiempo vecino corre más rápido que el de la nave.

La consecuencia evidente es que ese adelanto se debe a como medimos el tiempo desde la nave (los observadores de S’). Cuando partimos de la Tierra pasamos por un período de aceleración hasta alcanzar nuestra velocidad de crucero (al comenzar este capítulo suponíamos que lo logramos en un dia) y es durante este período cuando debe cambiar nuestra manera de ver el tiempo y la simultaneidad. Se dice que ha cambiado nuestra escala de tiempo.

Realmente Albert no ve nada de esto. Cuando afirmamos que “ve los sucesos que tiene delante alejarse en el futuro” lo que estamos diciendo es que cambia de observadores. Aunque decimos que es lo que se ve desde su nuevo sistema de referencia, no lo ve él sino sus observadores.

Al llegar a la estrella ocurren cosas similares. Frena, con lo que vuelve a S y vuelve a ver los relojes de S sincronizados, pero después acelera en sentido contrario para regresar a la Tierra.

Evidentemente vuelve a suceder lo mismo, los relojes de delante nuestro (ahora la Tierra está delante nuestro porque comenzamos el viaje de vuelta) se ven adelantarse, etc. Pero de todo lo visto, lo que más nos interesa recalcar es que estos cambios son ilusorios, no vemos el futuro de la Tierra, lo ven nuestros observadores. Si decidimos frenar de nuevo y volver a dar media vuelta, el cambio se deshace también.

Es decir, al cambiar de observadores (al iniciar el viaje de vuelta) los relojes de S se adelantan, pero sólo “en potencia”, es decir, si Albert continúa en el sistema S” y viaja hacia esos relojes.

Este cambio sólo pasará a serlo “de hecho” si Albert continúa ese viaje de vuelta (si no sale de S”). Si es así, a medida que se vaya encontrando con los relojes de S, comprobará que van muy adelantados.

Es importante tener claro que Albert no ve cambios importantes en su entorno inmediato durante el frenado y la aceleración. Los cambios residen en el sistema de referencia, o sea en los observadores, concretamente en los observadores alejados, aquellos que no ve, con los que no puede intercambiar información fácilmente precisamente por estar lejos.

Los cambios en su sistema sólo se materializarán si continúa el viaje durante el tiempo suficiente. En este sentido los cambios son aparentes o “en potencia” pues lo único que ha cambiado es su conjunto de observadores.

Dado que Albert no ve nada hasta que ocurre a su lado, podemos resumir lo que ve, lo que él experimenta, diciendo simplemente que su tiempo pasa más despacio, cosa que ya sabíamos al comenzar este apartado.

Pero también podemos decirlo de otra manera. Veamos como funciona el tiempo para Albert.

En cualquier viaje podemos recorrer el espacio en un sentido o en el contrario, pero el tiempo no, el tiempo sólo puede ir hacia adelante.

Dentro de la nave todos los relojes, tanto físicos como biológicos irán mas despacio que en la Tierra, por tanto como todo irá al mismo ritmo nadie se dará cuenta. Sólo los de fuera (los de S) verán la lentitud de todo lo que ocurre dentro de la nave.

¿Quién lo verá? Los observadores de S.

Lógicamente desde dentro, al mirar por la ventanilla verán el tiempo de S correr más rápido que el suyo, pero esto es así porque no estarán viendo el tiempo de la Tierra (que va más lento) sino el tiempo vecino, que va más rápido.

Por tanto desde dentro se tendrá la sensación de viajar hacia el futuro.

Exagerando un poco más para verlo más claro: si pudiéramos ir a 299 999 km/h nuestro tiempo (dentro de la nave) correría 387 veces más lento que fuera de la nave, o lo que es lo mismo, en un día de viaje daríamos un salto de 387 días en S.

Luego podemos considerar los viajes a velocidades próximas a la de la luz como saltos hacia el futuro. Exagerando más, en un viaje de cuatro meses daríamos un salto de más de cien años en S.