A.7. La paradoja de los gemelos, 2^a parte.

Lo más importante de la paradoja de los gemelos es que nos parece muy real ya que en breve podremos realizar largos viajes y posiblemente a velocidades elevadas, con lo que la dilatación temporal se hará palpable.

Desde el punto de vista científico esta paradoja tiene otro aspecto importante, y es que pone en evidencia que los cálculos relativistas solo son sencillos cuando tenemos dos sistemas en movimiento relativo uniforme. 

Afortunadamente en estos problemas más complicados los diagramas de Minkowski demuestran de nuevo su gran potencia.

A.7.5.  Tren de naves o tren de observadores de S’.

Todos imaginamos el sistema de referencia de la Tierra (S) como quieto, mientras que imaginamos a la nave (y por tanto a todo su sistema S’) en movimiento. Sin embargo ya dijimos que en R.E. no hay sistemas privilegiados, y esto significa que si lo imaginamos al revés (considerar la nave quieta y la Tierra moviéndose) todo debe funcionar igual.

La mejor imagen que podemos hacernos de la situación es la que planteábamos en el apartado A.5.1, donde imaginábamos dos trenes muy largos uno al lado del otro. Lo interesante de este modelo es que si no vemos ninguna referencia fija (árboles, vías, estaciones, ...), es decir, si sólo vemos lo que ocurre dentro de nuestro tren y lo que ocurre en el tren de al lado, resulta imposible establecer si estamos en movimiento o quietos o incluso si vamos en dirección contraria de la que parecemos llevar.

La imagen de los dos trenes nos permite ver lo relativo que es el concepto de movimiento y el de velocidad, y esto es justo lo que necesitamos tener claro ahora.

El sistema S’ va con la nave, se mueve con ella siempre a la misma velocidad. Tiene su origen quieto en un punto de la nave, por ejemplo la sala de mandos donde se encuentra nuestro astronauta, y por tanto respecto a S’ la nave no se mueve, es decir, está siempre en x’=0. Visto desde S’ para la nave la posición no cambia, pero el tiempo si va pasando, de ahí que su línea-mundo sea el eje de tiempos (verde).

Imaginar a los observadores de S’ es más difícil, por cuanto la nave de Albert es de por sí un objeto relativamente pequeño. En un viaje real Albert no tendría nunca esos observadores.

Sin embargo nosotros estamos haciendo un “experimento mental” al estilo de Einstein, así que nos podemos plantear cosas difíciles de realizar (por complicadas, por caras, ...) mientras sean posibles. Así pues vamos a concretar como podría ser el conjunto de observadores del astronauta A, ya que de ello depende entender el significado de la dilatación temporal que Albert ve en la Tierra. Es el concepto fundamental para entender cuando las situaciones son simétricas y cuando dejan de serlo.

Un observador de Albert debe ser necesariamente un humano que viaja a la misma velocidad que él y en la misma dirección y que además mantiene siempre su reloj sincronizado con el de Albert.

La mejor idea para imaginar tal cosa es imaginar un “tren de naves” que viajan constantemente por nuestra galaxia en la misma dirección que Albert y, aunque en la realidad esto sería absurdo, debemos imaginar que no paran nunca. Cuando uno de los “vagones-nave” pasa junto a la Tierra tenemos la posibilidad de subir al tren, y cuando pase junto a la estrella (E2) tenemos la posibilidad de bajarnos del tren.

El tren de naves materializa lo que entendemos por conjunto de observadores de A, uno en cada posición del espacio que separa la Tierra de la estrella. Cada uno quieto en un vagón determinado y provisto de su cinta métrica y su reloj sincronizado.

Según esto debemos imaginar que el vagón que pasa junto a la Tierra a los 5 años lleva muchos años viajando en la misma dirección que Albert y que siempre ha llevado su reloj sincronizado con el de Albert. Es uno de los vagones de cola del tren en el que se subió Albert hace 5 años.

Como hemos dicho, aunque ellos se vean sincronizados, desde la Tierra no lo verán así.

Los datos importantes del viaje de ida son los siguientes:

En resumen, volvemos a constatar como en ejemplos anteriores que los dos sistemas tienen métodos distintos para medir espacios y tiempos. Esto se materializa en el diagrama de Minkowski por el uso de ejes distintos.

Hasta aquí la situación es simétrica, pero ahora dejará de serlo pues Albert frena y da media vuelta para volver a la Tierra. Veamos que ocurre durante la vuelta.

A.7.6.  Análisis del viaje de vuelta:

Dado que una nave pequeña y aislada no es un buen modelo para materializar un sistema de referencia extenso y con observadores en todas partes, hemos decidido usar el modelo del tren de naves que circula constantemente por la galaxia recogiendo y dejando pasajeros pero sin parar nunca en ninguna parte (hay que subir en el tren en marcha).

Tras llegar a la estrella (suceso E2), Albert se baja del tren de ida y coge el de vuelta que es otro tren similar al anterior (S” en rojo en las Fig. 7.3 y 7.5) que hace constantemente el viaje de regreso de la estrella a la Tierra. Esto significa que deja de hacer caso a los observadores que iban en el tren S’ (en verde en los diagramas) y a partir de ahora escuchará lo que le digan los del nuevo tren S” (en rojo). Como veremos esto marcará la diferencia y romperá la simetría de la situación.

Aunque podemos pensar que sería mejor hacer girar el sentido de viaje a todo nuestro tren, esto nos conduciría a razonar mal pues nos haría olvidar que siguen existiendo tres sistemas de referencia, nos escondería todos los efectos que tiene el cambio de sentido y mucho más importante, como veremos un poco más adelante... ¡es imposible!.

De momento nos despreocuparemos del período de frenado o desaceleración que necesita Albert para bajarse del tren que se aleja de la Tierra y del proceso de aceleración necesario para subirse al tren que regresa a casa. Algunos autores dan mucha importancia a estas aceleraciones, y en un viaje real la tendría, pues si no queremos matar a Albert la aceleración debe ser suave y esto implica que durará mucho tiempo (posiblemente años), sin embargo nosotros idealizaremos el proceso para no tener que estudiar movimientos acelerados.

Supongamos que se haya descubierto algún proceso para proteger a los astronautas de los efectos de las elevadas aceleraciones y que podemos frenar en un período muy corto de tiempo (por ejemplo un día) visitar la base permanente en aquel sistema estelar, cumplir nuestra misión allí (en otro día) y volver a acelerar en sentido contrario rápidamente (en un tercer día), de manera que el tiempo invertido en todo este proceso (tres días) sea despreciable frente a los años invertidos en el viaje.

Cuando Albert visite la estación estelar comprobará que su reloj marca 3 años mientras el de la estación marca 5, conforme a lo que hemos deducido en el apartado anterior (A.7.4).

Por el hecho de abandonar el tren de ida ha dejado de confiar en los observadores que iban en aquel. Aunque el vagón del que acaba de bajar sigue casi idéntico a cuando lo dejó (los observadores que le acompañaban tienen relojes que marcan 3 años como el suyo propio), hora se encuentra en S, y por tanto ve ese tren (S’) mal sincronizado.

Durante el breve tiempo que dura su visita ve las cosas como se ven en S y por tanto ve que en la Tierra han pasado 5 años. De hecho si su visita es breve no tiene tiempo de ver gran cosa, pues las señales procedentes de la Tierra tardan años en llegar, pero ve que todo encaja con esa escala de tiempos. Si no tuviera prisa por volver y pasase unos años en la base estelar comprobaría que así es.

Pero Albert debe volver enseguida hacia la Tierra, así que al tercer día enciende los motores de su nave para acelerar y subirse al tren de vuelta. Tal como decíamos, supondremos que la aceleración es muy rápida y que el tiempo invertido en cambiar la dirección del movimiento (un día) es suficientemente breve como para despreciarlo al compararlo con los 10 años (casi 3700 días) que dura el viaje.

Ahora la situación es muy parecida a la inicial. Albert se encuentra en la estrella junto a los observadores (de S) residentes allí e inicia un viaje similar al anterior para cubrir la misma distancia a la misma velocidad pero en sentido contrario.

Lógicamente el tiempo necesario para el viaje es el mismo, 5 años, y la distancia recorrida en este tiempo es la misma que a la ida, 4 al, pero igual que antes él sólo ve un trayecto de 2,4 al y un tiempo de 3 años.

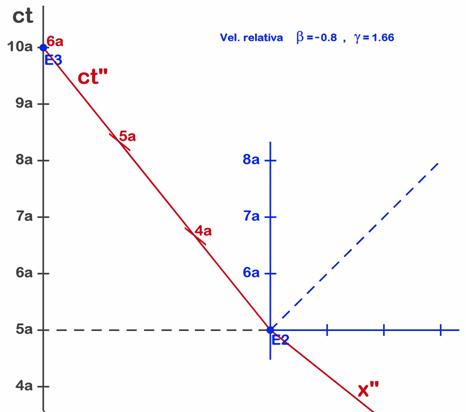
Dibujamos un nuevo diagrama de Minkowski (Fig. 7.5) con origen en la base estelar E2 de donde sale el viaje de vuelta.

Los ejes azules son los del sistema S, pero ahora situados en la estrella. Aunque parezca que son ejes distintos, son los mismos de los diagramas anteriores, pues el eje de tiempos es vertical como el eje negro y el de espacios horizontal, y si comenzamos a medir tiempos a partir de 5 años (que es el tiempo de la Tierra), los dos ejes medirán exactamente lo mismo, son sistemas de medida idénticos, aunque situados en puntos y momentos diferentes.

La asimetría viene de que la forma con que mide el astronauta si cambia, pues cambia su velocidad, y por tanto su viaje de vuelta viene representado por nuevos ejes (rojos).

Fig. 7.5 -  El viaje de vuelta es muy similar al de ida.

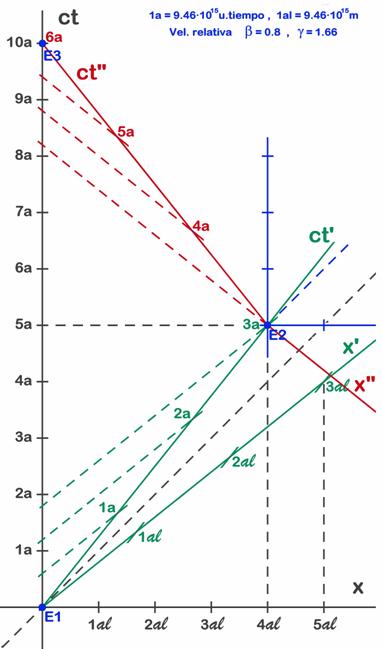
El eje importante ahora es el de tiempos (rojo), que igual que antes representa el trayecto de vuelta desde E2 (la estrella) a E3 (la Tierra). Dado que sabemos que el viaje dura 5 años y recorre 4 al (aunque hacia la izquierda), no insistiremos en como trazar los ejes: unimos esos dos puntos y sabemos que para el astronauta son 3 años, así que trazamos tres divisiones.

Sobre el nuevo eje de tiempos rojo en lugar de comenzar a medir tiempos (t”) desde cero comenzamos desde 3 años para que encaje con el gráfico anterior, o sea con el reloj del astronauta A. En el eje de espacios rojo (x”) no marcamos unidades porque no las necesitamos.

A la izquierda hemos dejado el antiguo eje de tiempos de la Tierra (S), pues nos interesa comparar lo que ocurre en la nave (Albert) con lo que ocurre en la Tierra (Tom). Ya hemos dicho que los ejes azules nuevos representan lo mismo que los negros, pues son paralelos a aquellos y dan las mismas medidas que aquellos.

El viaje completo ya lo habíamos representado en la figura 7.3, pero también lo podemos ver en la figura 7.6, donde usaremos el diagrama, con nuevas líneas de lectura, para analizar lo que ve el astronauta durante la vuelta y durante el cambio de sentido.

Cuando para Albert ha pasado 1 año, la línea de lectura verde nos dice que ve sólo 0,6 de Tom (o de la Tierra). Cuando han pasado 2 años ve 1,2 para la Tierra, y así sucesivamente. Por cada año de Albert ve pasar 0,6 de Tom (líneas de lectura verdes de la figura 7.6).

Durante el viaje de vuelta Albert ve algo similar, por cada año de su reloj (de S”) ve pasar 0,6 de Tom (líneas de lectura rojas en la figura 7.6).

Por otra parte Tom que mira desde la Tierra, durante el viaje de vuelta ve transcurrir 5 años y ve un recorrido de 4 al, mientras que su hermano astronauta sólo ve pasar 3 años. El tiempo total del viaje de ida y vuelta, visto desde la Tierra es de 10 años, mientras para Albert es de sólo 6 años.

Es una diferencia suficientemente importante como para que los hermanos gemelos puedan notar un envejecimiento distinto al volverse a encontrar.

Fig. 7.6 -  Durante la ida Albert está en el sistema S’ verde y ve pasar
0,6 años, 1,2 años y 1,8 años en la Tierra. A la vuelta está en el sistema S”
rojo y ve pasar 8,2 años, 8,8 años, 9,4 años  y 10 años en la Tierra.

Observemos que sobre el diagrama queda claro que tampoco ven el mismo espacio recorrido. Para Tom el trayecto es de 8 al, mientras que para Albert sólo han sido 4,8 al debido a la contracción de longitudes.

Los valores utilizados en el diagrama 7.6 son:

Todo esto se puede ver en el diagrama conjunto (Fig. 7.6), pero lo volveremos a discutir con más detalle más adelante.