A.7. La paradoja de los gemelos, 1^a parte.

La R.E. representó una auténtica revolución y rompió muchos esquemas, pero sin duda el cambio más importante fue el de romper nuestro concepto de tiempo absoluto.

La inversión temporal y la paradoja del garaje resultan llamativos, pero son problemas rebuscados que solo interesan en medios académicos porque no afectan a nuestra vida cotidiana.

Sin embargo la llegada a la Luna inició la era de los viajes espaciales y estos, poco a poco, han vuelto reales o al menos posibles conceptos que antes se consideraban de ciencia-ficción como los viajes a otras estrellas, las velocidades próximas a la de la luz o los agujeros de gusano.

La paradoja de los gemelos ha hecho correr ríos de tinta por dos motivos, el primero es su carácter paradójico, pero el segundo y más importante es que nos parece muy real ya que en breve podremos realizar largos viajes y posiblemente a velocidades elevadas, con lo que la dilatación temporal se hará palpable.

Desde el punto de vista científico esta paradoja tiene otro aspecto importante, y es que pone en evidencia que los cálculos relativistas solo son sencillos cuando tenemos dos sistemas en movimiento relativo uniforme. Veremos que la R.E. no dispone de mecanismos sencillos para estudiar sistemas acelerados ni cambios de velocidad de sistemas de referencia (es casi lo mismo).

Afortunadamente en estos problemas más complicados los diagramas de Minkowski demuestran de nuevo su gran potencia.

A.7.1.  Motivación de la paradoja de los gemelos.

Sabemos que según la relatividad, en dos sistemas que estén en movimiento relativo el uno respecto al otro, los observadores de cada sistema ven los relojes del otro ir más despacio (dilatación temporal). Como decíamos al estudiar los diagramas de Minkowski para la dilatación temporal, el problema está en que ambos sistemas usan escalas de tiempo distintas y no comparables (una no es mayor ni menor que la otra) más que para sucesos concretos.

Sin embargo podemos imaginar situaciones en las que los observadores de uno y otro sistema se vuelvan a encontrar, de manera que podamos comparar sus relojes poniéndolos uno al lado del otro.

Según la manera elegida para hacer que se vuelvan a encontrar los resultados serán distintos. Podríamos hacerles recorrer una órbita circular yendo ambos en direcciones contrarias hasta volver a encontrarse, o hacer que ambos se alejen primero (respecto a un punto de referencia considerado inmóvil) y después inviertan su movimiento para volver a encontrarse en el punto de partida. El estudio detallado de estas y muchas otras alternativas puede resultar muy complicado, pero os podemos adelantar la respuesta para estos dos casos: en ambos casos la simetría de la situación nos permite afirmar que al volverse a encontrar ambos relojes marcarán el mismo tiempo

Sin embargo estudiar con detalle situaciones como estas puede resultar muy complicado porque en todos ellos aparecen en algún momento aceleraciones (frenar es también una aceleración) y en R.E. no tenemos medios sencillos para tratar el movimiento acelerado.

Así pues elegiremos la formulación más sencilla posible y después ampliaremos el tema comentando algunas limitaciones para llevarla a la práctica y veremos también como esta paradoja pone en evidencia algunas limitaciones para los cálculos relativistas, especialmente para tratar las aceleraciones.

A.7.2.  Enunciado de la paradoja de los gemelos.

Suponiendo que algún día sea posible realizar viajes a otros sistemas estelares a velocidades próximas a la de la luz, nos planteamos calcular como transcurrirá el tiempo para los astronautas que realicen el viaje comparado con el tiempo de los demás humanos que permanezcan en la Tierra.

Para concretar y poder hacer cálculos (gráficamente) supondremos que el viaje se realiza a una velocidad de 0,8 veces la velocidad de la luz ( o sea velocidad del 80 % de c). En la tabla 1 (A.4.2) podemos ver que esto corresponde a una velocidad de 240 000 km/s. Hay que aclarar que estas velocidades puede que no se alcancen nunca, y no sólo por la dificultad técnica que puedan presentar, sino porque exigirían una cantidad de energía desorbitada y sobretodo porque serían muy peligrosas (la colisión con pequeñas partículas de polvo a esa velocidad calentará enormemente la nave y puede agujerear el casco más duro imaginable).

A esa velocidad (diremos simplemente ), la duración prevista del viaje (visto desde la Tierra) a una estrella que se encuentre a 4 años-luz (al) como Alfa-Centauri es de 5 años de ida y 5 años de vuelta. Despreciaremos el tiempo necesario para cumplir la misión que tengan encomendada y consideraremos que la nave regresa enseguida a la Tierra.

Supondremos que el astronauta, al que llamaremos Albert, o A, sale de la Tierra con un reloj sincronizado con el de la estación espacial en el instante t = t’ = 0.

Supondremos también que Albert deja en la Tierra un hermano gemelo al que llamaremos Tom, o T que, al tener un cuerpo genéticamente idéntico al de Albert, nos permite materializar de forma muy patente el concepto de reloj biológico y la idea del envejecimiento relativo de uno respecto al otro.

Hoy en día es del dominio público que al volver el astronauta (A) será más joven que su gemelo, pues para él habrá transcurrido menos tiempo que para el hermano que ha permanecido en la Tierra (T). La idea más extendida es que eso es debido a la elevada velocidad.

Sin embargo deberíamos preguntamos cómo es posible esto, ya que si A se mueve respecto a T resulta que T se mueve respecto a A con la misma velocidad. ¿No hemos quedado que las transformaciones de Lorentz son simétricas? ¿No hemos dicho que todos los sistemas inerciales son equivalentes?

Si usásemos las ecuaciones de Lorentz para calcular el tiempo de cada uno de los gemelos veríamos que el cálculo parece muy arbitrario, nos deja con la sensación de que efectuando los cálculos de otra manera obtendríamos que el más joven es Tom, el gemelo de la Tierrra (T).

Resolver este problema sólo con ecuaciones y sin los diagramas de Minkowski hace muy difícil interpretar los resultados y nos deja con una desagradable sensación de arbitrariedad.

Nosotros razonaremos sobre un diagrama de Minkowski y veremos claramente que es el hecho de cambiar de sistema inercial lo que genera la diferencia de tiempos entre ambos hermanos, aunque el cambio temporal no se produce instantáneamente, como muchos creen. La discusión de los detalles de este problema es casi imposible sin el adecuado diagrama de Minkowski.

A.7.3.  Calibrando el diagrama de Minkowski.

Dado que hemos cambiado de velocidad los diagramas usados en los capítulos anteriores no nos sirven y deberemos construir y calibrar unos nuevos.

Hemos elegido una velocidad relativa  , y por tanto la pendiente de nuestra recta deberá ser de 0,8. Para trazar los ejes verdes marcamos los puntos de pendiente siguientes: sobre el x=1 un punto de altura 0,8 y sobre el punto x=2 un punto de altura doble 1,6.

Una vez trazados estos ejes los calibramos usando el factor gamma que obtenemos de la tabla 1 (ver A.4.2). Dado que  deberemos dibujar una vertical sobre x=1,667 y al cortar el eje verde obtendremos la unidad del eje verde,  encima de 3,333 tendremos la segunda unidad y encima de 5 la tercera (Fig. 7.2).

 
Fig. 7.1 -  Calibramos el diagrama.

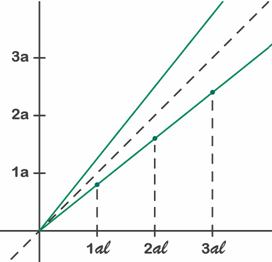
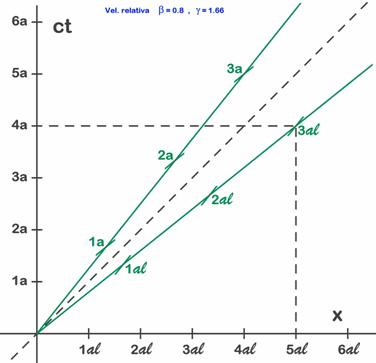
Lo más práctico es ir directamente al valor x=5 que nos permite trazar la pendiente tomando altura 4 y nos permite marcar la tercera unidad (Fig. 7.2). Graduaremos los ejes en años-luz y años, ya que las otras unidades resultan demasiado pequeñas para este problema.

Hay que repetir este proceso dos veces, una para dibujar y calibrar el eje x’ y otra para el eje t’ (o mejor ct’), que como ya sabemos son totalmente simétricos.

Al haber elegido una velocidad mayor la dilatación temporal será más pronunciada y los efectos sobre la nave y el astronauta serán más notables.

Fig. 7.2 -  Para la paradoja de los gemelos usamos velocidad  0,8 c.

Podemos calibrar los ejes usando como referencia el punto (5,4).

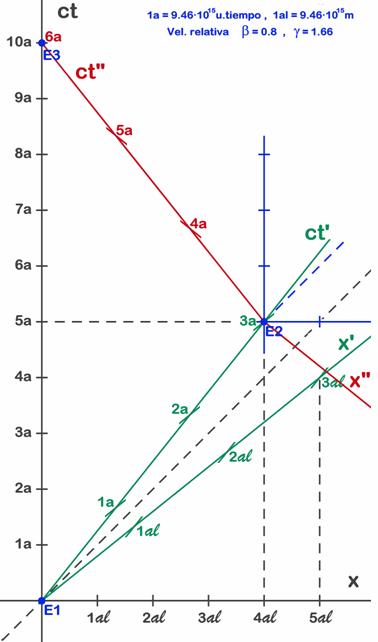
Si se va a dibujar estos ejes con ordenador puede ser útil saber que el ángulo de los ejes verdes es de 38,66º, ya que la mayoría de programas de dibujo permiten rotar objetos indicando el ángulo a girar.

El viaje tendrá un tercer sistema de referencia a partir del momento en que el cohete da media vuelta y comienza el viaje de regreso (véase la Fig. 7.3).

Aunque hasta ahora nunca habíamos utilizado diagramas con ejes que no arrancan del origen, veremos que no introducen ninguna complicación. Hay que tener presente que si queremos que quede reflejado el tiempo del astronauta en los ejes, estos terceros ejes deberán comenzar a contar a partir de 3 años, pues cuando comenzamos a usarlos el astronauta ya lleva 3 años de viaje.

Otra dificultad en este diagrama es que cuando comienza el viaje de retorno usamos para el cohete una velocidad hacia la izquierda. Si hiciéramos cálculos con fórmulas simplemente pondríamos v=-0,8c , pero en el diagrama significa que el eje de tiempos (rojo) está inclinado hacia la izquierda. Sin embargo el tiempo sigue corriendo en sentido positivo (el tiempo siempre avanza), o sea hacia arriba como en los ejes temporales de todos los gráficos anteriores.

Análogamente la dirección positiva del eje de espacios debe ir hacia la derecha como todos los ejes de espacios, pero en este caso el eje x” (rojo) está inclinado hacia abajo.

Ya que tenemos tres pares de ejes sobre el mismo diagrama puede ser interesante observar la simetría de estos. Vemos que siempre se abren de forma simétrica respecto a la línea de luz (bisectriz del primer cuadrante).

Sabiendo que la velocidad es la misma que para el viaje de ida (ejes verdes), utilizaremos las mismas unidades para el eje temporal rojo que las que hemos usado para los ejes verdes y no nos molestaremos en repetir todo el proceso de calibrado. Podríamos calibrar igual el eje espacial rojo (x”), pero no lo hemos calibrado porque su parte positiva se sale de nuestro diagrama y no lo necesitamos en nuestra exposición.

El diagrama del viaje será el siguiente:

Fig. 7.3 -  Los dos tramos del viaje del gemelo astronauta (A).

Donde el eje de tiempos verde es a la vez la línea‑mundo del astronauta A en su viaje de ida, que termina en el punto E2 (x=4 al , ct=5 a).

El punto E2 es el final de la primera parte del viaje. Representa el suceso ocurrido a los 5 años cuando llega a la estrella que se encuentra a 4 años-luz de distancia (visto desde el sistema S o de la Tierra).

Hemos prolongado ese eje después de la llegada (y podríamos haberlo hecho antes del punto de partida, hacia tiempos negativos) porque nos interesa pensar en el sistema S’ (el conjunto de observadores en todos los puntos de S’ con relojes sincronizados) después de que el astronauta A (supondremos que con su nave incluida) lo haya abandonado para iniciar el viaje de vuelta.

Supondremos que inmediatamente después de llegar a la estrella el astronauta comienza el viaje de regreso a la Tierra.

Esta segunda parte del viaje está representada por la línea roja, que también es a la vez el eje temporal del sistema S” y la línea-mundo del astronauta A en su viaje de regreso a la Tierra. La velocidad de este viaje de vuelta es la misma que a la ida, pero en sentido contrario (v=–0,8).

El viaje termina en el punto E3 (x=0 al , ct=10 a), que representa el suceso de llegar de nuevo a la Tierra (que siempre se encuentra en x=0) en el instante 10 años.

En los apartados siguientes estudiaremos detalladamente estos dos tramos y en particular intentaremos ver porqué se dilata el tiempo del astronauta A y no el del terrícola T. Nos preocupa especialmente entender porque las leyes de la R.E. parecen dejar de ser simétricas y los dos sistemas inerciales parecen no funcionar igual.

A.7.4.  Análisis del viaje de ida.

Durante el trayecto de ida la nave se mantiene en el sistema S’ (verde) y todo el sistema se mueve con ella. Respecto a S’ la nave no se mueve, es decir, está siempre en x’=0. Visto desde S’ para la nave la posición no cambia, pero el tiempo si va pasando, de ahí que su línea-mundo sea el eje de tiempos (verde).

Al cabo de 3 años de su tiempo (el ct’=3 del eje de tiempos verde) llega a la estrella de destino. Es el suceso E2 marcado como un punto azul en los diagramas de las figuras 7.3 y 7.4.

Vemos que en su sistema sigue estando en x’=0, pero que la coordenada temporal ha cambiado a t’=3, luego para Albert desde que salió de la Tierra (suceso E1) hasta que llega a su destino (suceso E2) han transcurrido 3 años.

¿Cómo se ve el viaje desde la Tierra?

Para calcular lo que se ve desde el sistema S (de la Tierra) trazamos las líneas de lectura horizontal y vertical y obtenemos t=5, x=4.

Esto significa que Tom (T) desde la Tierra ve transcurrir 5 años para el viaje de ida, tiempo en el que ve como su hermano astronauta Albert (A) ha recorrido una distancia de 4 al. 

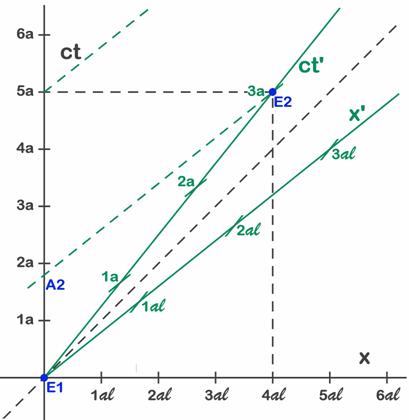
Hasta aquí el viaje debería ser simétrico, y así es. Si miramos el tiempo que pasa para la Tierra visto por el astronauta Albert obtendremos también una dilatación temporal. Por el punto E2 trazamos una paralela al eje verde de espacios y vemos (Fig. 7.4) que corta al eje de tiempos de S en 1,8 años (línea de lectura verde que corta en A2). Esto significa que aunque Albert lleva 3 años de viaje, si mira el reloj de la Tierra ve que allí sólo han pasado 1,8 años.

Aprovechamos este ejemplo para aclarar que cuando decimos que “Albert ve” o que “Tom ve” nos referimos a lo que ven sus observadores ya que

En las conclusiones de este capítulo volveremos a discutir el problema de tener que fiarse de sus observadores, y veremos que cambiar de sistema es cambiar de observadores y ambas cosas van unidas indisolublemente a la escala de tiempo en la que elegimos vivir. Pero conviene aclarar el papel de los observadores en ambos sistemas para poder entender después la importancia del cambio de observadores.

Que Tom tenga observadores en la estrella (que no se muevan respecto a la Tierra) es fácil de aceptar, pues puede haber colonias humanas que ya se han establecido previamente allí. Cuando Albert llega a la estrella los observadores del sistema S le dirán que han pasado 5 años y le dirían lo mismo tanto si se detiene como si continua en la misma dirección.

Esto no cuadra muy bien con lo que le dice su observador en la Tierra, que le dice que allí sólo han pasado 1,8 años.

Fig. 7.4 -  Durante el viaje de ida ambos ven una dilatación temporal para el otro.

El problema es que aunque dentro de S los observadores (quietos respecto a la Tierra) se ven sincronizados, desde S’ no les ven sincronizados. Por ejemplo Albert (observando desde S’), que está llegando a la estrella, ve el reloj de allí (de S) que marca 5 años, mientras que el observador  (de S’) que tiene junto a la Tierra en ese momento ve allí que los relojes de la Tierra (de S) sólo marcan 1,8 años.

Lógicamente la simetría de la situación consiste en que desde S ven algo similar, ven los relojes de S’ mal sincronizados. A los 5 años, cuando Albert llega a la estrella un observador que está allí (en S)  ve a Albert (en S’) con un reloj que marca 3 años, mientras el propio Tom (que está en S) ve que el observador (de S’) que está junto a la Tierra lleva relojes que marcan 8,3 años.

En la Fig. 7.4 sólo hemos trazado un fragmento de la línea de lectura de este último tiempo (línea discontinua verde que arranca de 5a) porque se sale del gráfico. Ésta línea es paralela al eje verde x’ por el punto 5a del eje de tiempos negro, que es donde está la Tierra a los 5 años.

Si Albert continuase en el sistema S’, o sea si continuase alejándose de la Tierra a la misma velocidad, seguiría encontrándose con observadores de S que le dirían que ha pasado más tiempo en S que en el sistema de la nave (S’), pero los observadores de su propio sistema S’ le dirían lo contrario, que en la Tierra ha pasado menos tiempo que en la nave.

Los datos importantes del viaje de ida son los siguientes:

En resumen, volvemos a constatar como en ejemplos anteriores que los dos sistemas tienen métodos de medida de espacios y tiempos distintos, materializados en el diagrama de Minkowski por el uso de ejes distintos.

Hasta aquí la situación es simétrica, pero dejará de serlo en cuanto Albert frene y dé media vuelta para volver a la Tierra.

Antes de ver lo que ocurre durante la vuelta conviene aclarar un poco el concepto de observador, ya que es la primera vez que nos planteamos una situación asimétrica y aquí este concepto es fundamental.