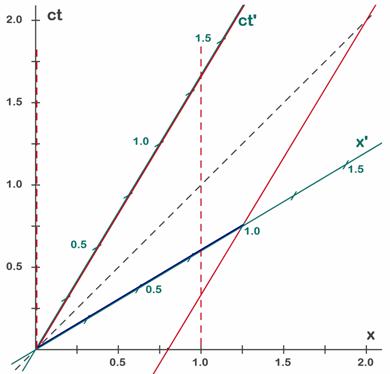
A.6. Inversión temporal y paradoja del garaje, 2^a parte

A.6.5.  Para S’ el coche no cabe en el garaje.

En los apartados anteriores hemos visto que para S’ el garaje mide 0,8 unidades y el coche 1 unidad, de forma que está claro que no cabe. Dibujemos ahora un diagrama de Minkowski en el que se vean ambos simultáneamente.

Fig. 6.6 -  Visto desde S’ el coche (barra azul de 1 u)  no cabe en el

garaje (verticales rojas a trazos) que sobre el eje verde mide 0,8 u).

En el diagrama (Fig. 6.6) el espacio del garaje es, igual que antes, el espacio entre las dos barras rojas verticales a trazos. La barra azul representa el coche en el instante inicial y claramente no cabe entre los trazos verticales.

Concluimos que los observadores de S’ ven una situación totalmente distinta de los de S.

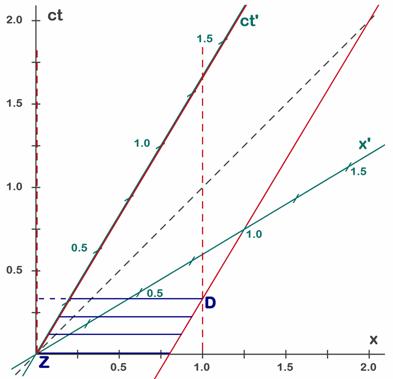
A.6.6.  La inversión temporal en el problema del garaje.

Aunque el resultado anterior está bastante claro no hemos observado la inversión temporal de la que hablábamos, ya que nos hemos centrado en las dimensiones de los objetos y no hemos mirado los instantes en que ocurrían las cosas.

Para ver la inversión temporal vamos a observar y medir los dos sucesos fundamentales del problema: el instante en que se cierra la puerta izquierda, justo cuando ha pasado todo el coche por esa puerta, y el instante en que hay que abrir la puerta derecha porque el coche empieza a salir por ella.

Podríamos usar el diagrama de la Fig. 6.5, pero preferimos repetirla y renombrar los puntos que ahora nos interesan.

En la Fig. 6.7 (casi idéntica a la Fig. 6.5) vemos que cuando lo miramos desde el punto de vista de S (observador en tierra firme) el coche entra en el garaje en t=0. Hemos marcado este suceso con la letra Z (por ser la puerta izquierda) y comienza a salir en el suceso D, o sea cuando t=0,33.

Fig. 6.7 -  La entrada del coche en el garaje termina al cerrar la puerta izquierda

(suceso Z). La salida comienza al abrir la puerta derecha (suceso D). Desde el

sistema S, se ve primero el suceso Z y 0,33 s después el suceso D.

El hecho de que la puerta derecha esté cerrada durante 0,33 s desde que se cerró la izquierda pone de manifiesto que el coche permanece cerrado un buen rato dentro del garaje (comparado con los tiempos que estamos manejando).

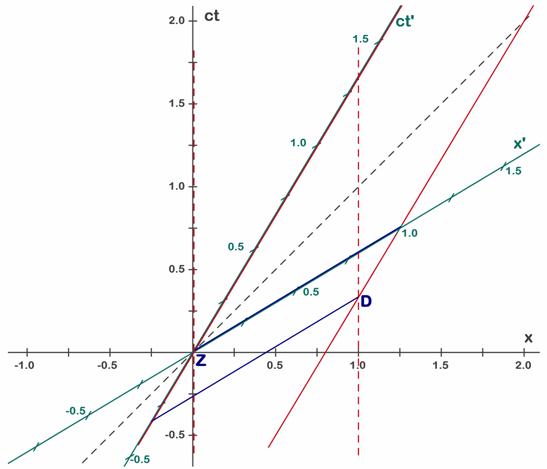
Para estudiar los tiempos vistos por S’ podríamos utilizar el diagrama de la Fig. 6.6, pero el eje negativo de tiempos se nos queda corto para representar el instante del suceso D, así que repetiremos ese diagrama modificando las letras y ampliando los ejes.

Los sucesos que nos interesan son los mismos: El suceso Z (Fig. 6.8) ocurre cuando la cola del coche pasa por la puerta izquierda y podemos cerrarla. En ambos casos coincide con el origen de coordenadas y para ambos ocurrirá en el instante cero (ahora hablamos del tiempo de S’ y escribiremos t’=0).

El suceso D ocurre cuando el morro comienza a salir por al puerta derecha. Representa la apertura de la puerta de salida. El suceso es el mismo para ambos sistemas, pero no miden igual ni su la posición (pues los sistemas se mueven) ni el tiempo de este suceso.

Para S’ el instante del suceso D se mide trazando la paralela al eje verde de espacios. Es la línea azul de abajo (no estaba en la Fig. 6.6) que corta en –0,33 s. O sea que la puerta derecha debe abrirse en ese instante si no queremos que el coche choque contra ella.

Lo importante es que visto desde S’ la puerta derecha se abre antes de que se pueda cerrar la puerta izquierda, y el motivo es claro: el coche no cabe en el garaje.

Recordemos que en el gráfico el espacio del garaje es la distancia entre las dos líneas rojas verticales (a trazos) y el espacio ocupado por el coche es la distancia que separa las líneas rojas oblicuas. Visto para S’ el coche es la barra azul y claramente no cabe entre las líneas discontinuas rojas (el garaje).

Fig. 6.8 -  Visto desde S’ el coche (barra azul de 1 u)  no cabe en el

garaje (verticales rojas a trazos) que sobre el eje verde mide 0,8 u).

Resumiendo los resultados vistos desde el sistema S’ vemos que el suceso D (abrir la puerta derecha) es anterior al suceso Z (cerrar la puerta izquierda).

Pero lo que resulta más llamativo aquí es que se ha producido una inversión temporal, o sea, que los sucesos que en S se ven en un orden (primero Z y después D), en S’ se ven en el orden inverso (primero D y después Z).

Esta situación de inversión temporal produce una sensación paradójica. Parece que contradice la lógica y sin embargo es inevitable si dos sistemas miden los tiempos de diferente manera.

Con los diagramas de Minkowski no sólo constatamos este efecto, sino que somos capaces de medir esos tiempos y concretar lo que verán desde cada sistema en cada momento.

A.6.7.  La inversión temporal y la causalidad.

A primera vista la inversión temporal parece absurda. Tendemos a pensar que dos sucesos cualesquiera se pueden invertir, y esto sí que sería absurdo, pues después de un desastre como romper un jarrón chino, podríamos pasar al sistema en que se ven los sucesos al revés y llegar a tiempo para detener la caída del jarrón.

La inversión temporal parece un viaje en el tiempo, pero no lo es. En R.E. cada sistema mide los tiempos de forma diferente, pero el tiempo nunca va hacia atrás.

Aunque no entraremos a fondo en el tema, intentaremos entender cuando cabe esperar y cuando no la inversión temporal.

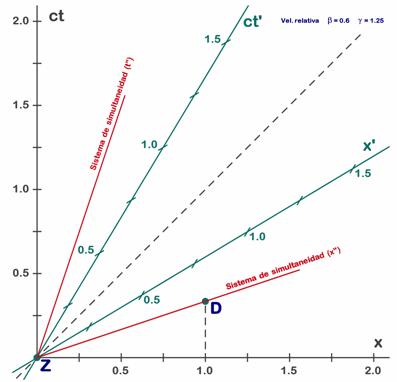
En el problema del garaje hemos visto que para S (tierra firme) Z ocurre 0,33 s antes que D, mientras que para el sistema S’ (dentro del coche) D ocurre 0,33 s antes que Z. Si elegimos el primero como patrón escribiremos el tiempo del segundo caso como –0,33 s.

Si ponemos otro coche al lado con una velocidad menor veremos que la diferencia de tiempos no es tan grande. Si la velocidad es elevada (próxima a la del coche) el tiempo entre los sucesos será parecido al que ve S’, pero menor, por ejemplo –0,20 s. En cambio si este nuevo coche va a baja velocidad, de manera que casi no se notan los efectos relativistas, su tiempo se parecerá al observado por S (tierra firme), por ejemplo 0,20 s.

Lo que estamos diciendo es que eligiendo una velocidad adecuada para el tercer coche podemos situarnos en un sistema que vea el desfase temporal que queramos, aunque sólo estamos afirmando esto para valores intermedios entre los dos observados (+0,33 s y –0,33 s).

Si aceptamos esto como cierto (no es difícil de ver, pero en una introducción como esta tampoco tiene excesivo interés ver más detalles) resulta evidente que habrá un sistema en el que la diferencia temporal entre los dos sucesos será de 0 s. Y en efecto es así.

El sistema en el que se ve tiempo nulo entre los sucesos (es decir Z y D se ven simultáneos) resulta ser el sistema que lleva una velocidad que sea exactamente la mitad de la de nuestro coche, o mejor dicho, el que queda justo en medio de ambos, viendo a ambos a la misma velocidad pero en sentidos contrarios. Esta velocidad resulta ser siempre un poco mayor que la mitad (en nuestro caso resulta ser de 0,33 c en lugar de 0,3 c) debido como siempre a que miden espacios y tiempos d forma diferente. Para esta velocidad lo que ocurre es que para este sistema el garaje y el coche de nuestro estudio se mueven a la misma velocidad pero uno al encuentro del otro. Desde este sistema todo es muy simétrico y la llegada del coche al garaje también.

Aunque no lo estudiaremos con detalle, afirmamos que la característica de los sucesos que se pueden invertir temporalmente es que en algún sistema ocurran simultáneamente (en el ejemplo anterior es el sistema del tercer coche, que va a la velocidad intermedia).

Elegir un sistema adecuado es elegir la velocidad adecuada para ver la simultaneidad. A esa velocidad le llamaremos velocidad de simultaneidad (de esos dos sucesos).

Sobre los diagramas de Minkowski la velocidad era la pendiente de la recta temporal y esta condición se traduce en que se pueda dibujar un eje de espacios que una estos dos sucesos.

Fig. 6.9 -  El sistema de simultaneidad para nuestros dos

sucesos Z y D casualmente pasa por el origen (en rojo).

Dado que sabemos que los ejes de espacios están por debajo de la línea de luz, sobre el gráfico la condición se traduce en que la inclinación de la línea que une ambos sucesos sea inferior a 45º (inclinación inferior a la línea de luz).

Si existe una velocidad de simultaneidad, como ocurre para los sucesos Z y D de nuestro problema, cualquier sistema que viaje más rápido, o sea que viaje en el sentido de Z a D (S’ en nuestro caso) verá D anterior a Z, mientras que cualquiera que vaya mas despacio, o sea que relativamente al sistema de simultaneidad vaya en el sentido de D a Z (o sea en sentido contrario al anterior) verá los sucesos en el orden contrario.

Lógicamente los sucesos en esta situación no pueden tener relación causal, cosa fácil de entender pues están tan lejos que ninguna señal puede llegar a tiempo del suceso Z al suceso D (ni a la inversa). Se dice que el intervalo que los separa es espacial porque en situación de simultaneidad lo único que les separa es espacio y porque no existe ninguna situación (ningún sistema) en la que lo único que les separe sea tiempo.

En el apartado siguiente completaremos nuestro estudio de la causalidad con el estudio de los intervalos temporales.

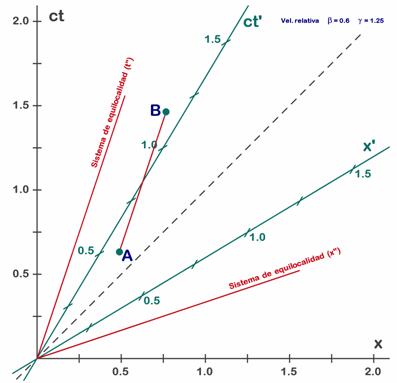
A.6.8.  El cono de luz y la relación de causalidad.

Hemos visto que los sucesos que se puedan unir con una línea inclinada (o intervalo espacial) con menos de 45º se pueden situar en un sistema en el que se ven simultáneos (sistema de simultaneidad)

Por el contrario los sucesos cuya línea de unión o intervalo tenga una inclinación de más de 45º no se podrán tener nunca esta relación de simultaneidad (mismo instante de tiempo), pero existirá un sistema en el que se verán suceder en el mismo lugar (equilocalidad) aunque en instantes diferentes.

Consideremos los sucesos A y B de la Fig. 6.10. La línea que los une tiene una inclinación de más de 45º. Trazamos una paralela por el origen y tenemos un eje de tiempos para el cual ocurren en el mismo lugar. Llamaremos S” a este sistema (en rojo) y en éste ambos sucesos ocurren en el mismo lugar, pues su posición se encuentra trazando paralelas al eje de tiempos, y dan la misma paralela.

Fig. 6.10 -  En el sistema de equilocalidad de nuestros dos

sucesos 1 y 2 (en rojo) ocurren en el mismo lugar.

Esta relación de equilocalidad (mismo lugar) nos permite asegurar que en cualquier otro sistema el suceso A siempre sucederá antes que el B, aunque en cada uno de ellos pueda suceder en un lugar distinto. Se dice que el intervalo que los separa es temporal porque en situación de equilocalidad lo único que les separa es tiempo y porque no existe ninguna situación (ningún sistema) en la que lo único que les separe sea espacio.

Mirando desde el punto de vista del suceso A se dice que B pertenece al futuro de A, pues en todos los sistemas ocurre después de A. Esto hace que B pueda ser un suceso ocasionado a consecuencia del suceso A. Si esto ocurre decimos que A es la causa de B.

Siempre que dos sucesos tengan relación causal la causa debe ocurrir antes que el efecto y por tanto debe existir un sistema de equilocalidad para estos sucesos. La relación de causalidad sólo puede existir entre sucesos separados por intervalos temporales.

La relación causa-efecto sólo puede existir si la causa está en el pasado del efecto, o lo que es lo mismo, si el efecto está en el futuro de la causa.

Gráficamente hemos dicho que esto significa que formen un ángulo de más de 45º. Si trazamos líneas de 45º sobre el suceso A veremos que sucesos pueden pertenecer a su futuro y cuales no.

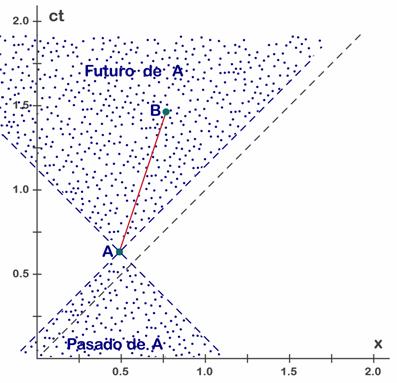
Fig. 6.11 -  El cono de luz delimita el pasado y el futuro del suceso A

y por tanto los sucesos que pueden tener relación causal con A.

La región punteada que queda por encima del suceso A (Fig. 6.11) constituye su futuro y los sucesos que caigan en esta región se pueden relacionar por un sistema de equilocalidad (en el que ocurren en el mismo lugar). En todos los sistemas todos estos sucesos pertenecen al futuro de A y por tanto alguno de ellos puede ser causado por A.

La región punteada inferior constituye el pasado de A. En cualquier sistema esos sucesos siguen estando en el pasado de A.

En todos estos casos, como hicimos con los sucesos A y B, podemos encontrar una velocidad de equilocalidad, esto es, un sistema en el que ambos sucesos ocurren en el mismo lugar y por tanto el intervalo que separa estos sucesos de A siempre es temporal.

Para este tipo de sucesos nunca podemos encontrar un sistema en el que sean simultáneos. El suceso B siempre está en el futuro de A, se mire desde el sistema que se mire (se mida como se mida el tiempo). Entre estos sucesos siempre hay una separación temporal y resulta imposible que entre ellos se produzca inversión temporal.