A.6. Inversión temporal y paradoja del garaje, 1^a parte

El concepto de causalidad es importante para nosotros y está indisolublemente ligado a nuestra idea de que el tiempo va en una dirección determinada y no puede ir al revés, pues la causa debe preceder al efecto.

Sin embargo en Relatividad el tiempo se mide de forma diferente en sistemas diferentes y esto puede dar lugar a situaciones paradójicas.

La paradoja del garaje se centra en el hecho de que medir tiempos de forma diferente puede hacer que cosas que se ven en un orden en un sistema (suceso A primero y suceso B después) pueden verse al revés en otro sistema (suceso B primero y suceso A después).

A esta situación se le llama “inversión temporal” y a primera vista nos parece muy absurda pues parece que en algún sistema se puede ver el efecto ocurriendo antes que la causa (el vaso roto en el suelo antes de que lo tiremos) y por tanto que en ese sistema se puede ver el tiempo yendo al revés que en el primer sistema.

Veremos que en efecto podemos ver sucesos en orden diferente, pero sólo en casos especiales, y nunca violando la ley de causalidad. El siguiente ejemplo es uno de los más conocidos.

A.6.1.  La paradoja del garaje.

Supongamos que un coche (si queremos ponerlo a grandes velocidades deberemos pensar más bien en un cohete) es un poco demasiado grande para entrar en un garaje, entonces podemos argumentar: si lo ponemos a altas velocidades su longitud se contraerá y cabrá en el garaje, aunque solo por una fracción de segundo.

Podemos concretar esto en el siguiente experimento imaginario:

Ponemos el coche a 180 000 km/s (la misma velocidad que usábamos en el capítulo anterior, así podemos aprovechar aquellos diagramas) y lo hacemos entrar por la puerta que hay en el extremo izquierdo del garaje. Durante una fracción de segundo el coche cabe en el garaje (debido a que se contrae) y podemos tener cerradas las puertas de los dos extremos del garaje. Inmediatamente después abrimos la puerta del extremo derecho para dejarlo salir, o de lo contrario a esta velocidad perforará la puerta o la pared que haya en el extremo derecho del garaje.

Todo parece claro y sencillo, pues ya hemos estudiado que a altas velocidades las longitudes se contraen, pero ya dijimos que estos efectos dependen del punto de vista.

En efecto, visto desde el coche (o el coche-cohete) las cosas se verán de otra manera. Ahora el observador es el conductor, que se mueve con el coche. Respecto a él el coche está inmóvil y según decíamos se puede considerar que el garaje es el que se está moviendo respecto a ellos.

El principio de Relatividad prevé que desde dentro del coche deben verse las mismas leyes de la física.

Pero si esto es así y consideramos que respecto al coche el que se mueve es el garaje, éste deberá contraerse, con lo cual el coche no cabrá dentro.

¿Cuál de los puntos de vista es el correcto? ¿Cabrá o no cabrá en el garaje?

La situación es paradójica pues estos dos puntos de vista parecen irreconciliables. Estamos acostumbrados a que no haya más que un punto de vista correcto, sin embargo en la Relatividad resulta que aunque nos sorprenda ambos son ciertos.

El observador de tierra firme que permanece junto al garaje verá como por un instante todo el coche cabe dentro del garaje, mientras que desde el coche verán encogerse el garaje y nunca verán todo el coche dentro del garaje.

A.6.2.  Desde el punto de vista de S el coche-cohete se contrae.

Hagamos un diagrama de Minkowski y estudiemos como es posible que vean cosas tan diferentes y aparentemente contradictorias.

Los ejes y unidades deberán dibujarse igual que en el capítulo anterior (apartados A.5.3 y A.5.4).

El vuelo del coche-cohete se representará como un objeto que se mueve con S’, tal como hacíamos en el ejemplo 3 (apartado A.5.7) en el que imaginábamos una barra de un metro moviéndose con S.

El diagrama resultante es el mismo de entonces, que reproducimos aquí:

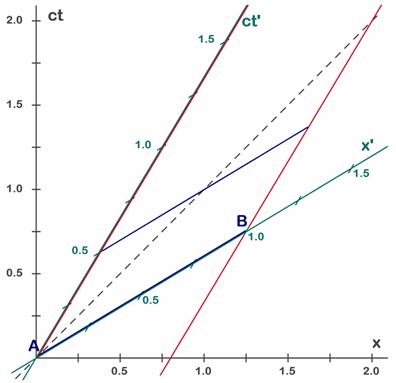
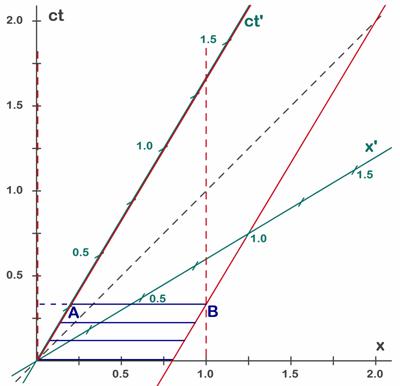
Fig. 6.1 -  El coche-cohete visto desde S’ viene representado por la barra

azul. Inicialmente (t’=0) se encuentra sobre del eje x’ (barra azul AB).

Para simplificar supondremos que el coche mide una unidad, ya que las dimensiones que tenga son indiferentes para nuestro razonamiento (en nuestro diagrama una unidad es un sl, por tanto es un coche-cohete muy largo). En el instante inicial el coche tiene su parte delantera o morro en B y sus cohetes (su parte trasera o cola) en A y se mueve con el sistema S’ hacia la derecha.

El movimiento del coche viene representado por las dos líneas rojas. Al cabo de medio segundo su posición es la indicada por la segunda barra azul. El hecho de estar un poco más arriba significa que es un instante posterior, que ha pasado un cierto tiempo, en este caso 0,5 segundos.

En el eje de tiempos de S’ (en verde) leemos un tiempo de 0,5 s y toda esta segunda barra azul se encuentra a esta misma altura y por tanto toda la línea azul se encuentra en el mismo instante de tiempo, debido a que está sobre una paralela al eje x’.

Visto desde S’ el coche no se mueve, ya que el extremo derecho o morro del coche siempre está en x’=1 (línea roja derecha) mientras que el extremo izquierdo que corresponde a los cohetes de cola siempre se encuentra sobre el eje de tiempos, que corresponde a x’=0.

La línea roja de la izquierda, que se encuentra sobre el eje de tiempos t’ representa la evolución temporal del extremo de cola del coche-cohete, mientras que la línea roja de la derecha representa el paso del tiempo del punto B, el morro del coche-cohete.

Visto desde S el coche se desplaza hacia la derecha y esto se refleja en que las líneas rojas están inclinadas respecto a los ejes negros. Para S tanto el punto A como el B (y por tanto todo el coche) se van desplazando hacia la derecha con el tiempo. Así el extremo derecho que está marcado con la letra B se encuentra en x=1,25, mientras que un poco más tarde (segunda barra azul) se ve más allá del 1,5 (aproximadamente en x=1,6).

Recordemos que el diagrama de la figura 6.1 representa lo que se ve desde S’, pero en S ven las cosas de otra manera.

La evolución de los extremos A y B se ve igual (las mismas líneas rojas), pero la simultaneidad se ve diferente.

Para mirar donde se ve el coche en el instante t=1 trazamos la horizontal a la altura 1 y encontramos los cortes A y B con las dos líneas rojas. Estas son las posiciones que se ven simultáneas para el sistema S y por tanto son las que determinan la posición del coche que verán desde S y la longitud que medirán desde S.

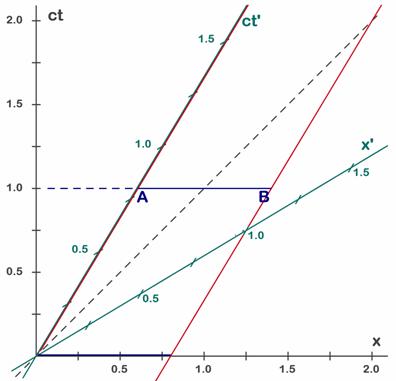
Fig. 6.2 -  El coche-cohete visto desde S viene representado por las barras azules.

Inicialmente (t=0) se encuentra sobre del eje x (barra azul de abajo) y mide 0,8 u.

Observamos que ambas barras horizontales miden 0,8 unidades (sl), mientras que en la figura 6.1 veíamos que el coche medía 1 unidad (visto desde S’). Esto significa que desde el punto de vista de S el coche se contrae, y es este efecto el que permitirá que el coche entre en el garaje (visto por los observadores de tierra firme o sea desde S).

A.6.3.  Desde el punto de vista de S’ el garaje se contrae.

Dibujemos ahora un nuevo diagrama de Minkowski para estudiar como se ve el garaje desde los dos sistemas.

Para no complicar el dibujo consideremos que coche y garaje miden (externamente) lo mismo y que el problema de que no quepa se debe a que las puertas tienen un pequeño grosor que hace que no se puedan cerrar simultáneamente las dos puertas con el coche dentro. Esto simplifica mucho nuestros cálculos, pues los valores a considerar son los mismos del diagrama anterior pero aplicándolos a los otros ejes.

Ahora el garaje está inmóvil respecto a S y mide 1 unidad (sl). Su evolución temporal en el sistema S se representa por las dos líneas rojas verticales de la Fig. 6.3.

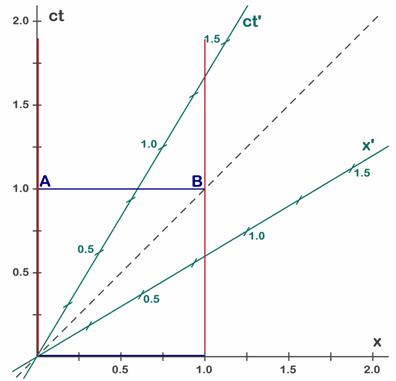
Fig. 6.3 -  El garaje visto desde S viene representado por la barra azul.

Inicialmente (t=0) se encuentra sobre del eje x (barra azul de abajo).

En todo momento la barra azul mide 1 unidad, lo cual se puede ver mirando las dos barras azules. En el instante inicial el garaje tiene su puerta derecha o de salida en x=1 y sus puerta izquierda o de entrada en x=0 luego mide 1 unidad.

Al cabo de 1 s ocupa la posición de la barra azul de arriba y tiene su puerta derecha o de salida en B, la línea de lectura vertical (roja) nos indica que seguimos teniendo x=1. La puerta izquierda o de entrada se encuentra en A, o sea sobre el eje de tiempos, por tanto x=0 luego sigue midiendo 1 unidad.

Este es el punto de vista de S.

La evolución temporal del garaje viene dado por la evolución temporal de sus extremos A y B, o sea por las dos líneas rojas.

El paso de la línea azul inferior a la línea azul superior representa el paso de 1 s, pero sólo cambia la escala de tiempo y no la posición espacial.

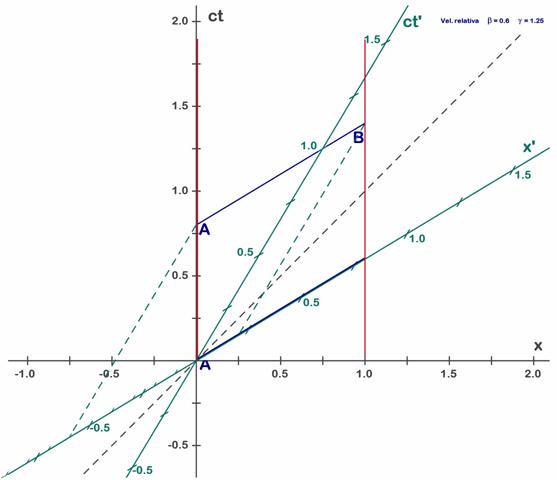
¿Cual es el punto de vista de S’?

Para S’ hemos dicho que el garaje se ve en movimiento. Haciendo medidas en dos instantes de tiempo diferentes podremos comprobarlo (véase la Fig. 6.4).

Si queremos saber donde está el garaje en el instante inicial (visto desde S’) deberemos trazar una paralela al eje x’ verde que pase por t’=0. La recta es el propio eje x’. El extremo izquierdo del garaje (la puerta de entrada) estará en el punto de esa recta que corte a la línea evolutiva del punto A, que es la línea roja de la izquierda. Observamos que en el instante inicial la puerta izquierda está en el origen, como ya sabíamos, pues lo hemos elegido así en el apartado anterior. La puerta derecha estará sobre la línea roja derecha, que es la línea temporal de la puerta derecha. Observamos que está sobre el eje x’ a 0,8 unidades del origen, por tanto esa es la longitud del garaje vista desde S’.

Para ver donde está el mismo garaje al cabo de 1 s debemos trazar una paralela al eje verde de espacios por la coordenada t’=1. Obtenemos la barra azul de arriba, que corta a las líneas evolutivas de ambos extremos en A y B. La longitud del garaje sigue siendo 0,8 unidades pero para S’ la barra  azul (el garaje) se ha desplazado hacia la izquierda 0,6 unidades. 

Fig. 6.4 -  El coche-cohete visto desde S’ viene representado por las barras azules.

Inicialmente (t’=0) se encuentra sobre del eje x’ (barra azul de abajo) y mide 0,8 u.

La posición de A se obtiene con la línea de lectura verde, que nos da x’=-0,6. Para B obtenemos x=0,2, aunque no hemos marcado las décimas en esa zona porque ya hay muchas líneas dibujadas.

A.6.4.  Para S el coche cabe en el garaje.

En las páginas anteriores hemos visto que para S el garaje mide 1 unidad y el coche 0,8 unidades, de forma que está claro que cabe. Dibujemos ahora un diagrama de Minkowski en el que se vean ambos simultáneamente.

Fig. 6.5 -  Visto desde S el coche (barras azules de 0,8 u) cabe

 en el garaje (verticales rojas a trazos, 1 u) durante 0,33 s.

En el diagrama (Fig. 6.5) el espacio del garaje es el espacio entre las dos barras rojas verticales (a trazos). Las barras azules representan el coche en diferentes instantes. El coche permanecerá dentro del garaje desde 0 s hasta 0,33 s. Vemos que las cuatro barras dibujadas quedan entre los límites de las puertas del garaje.