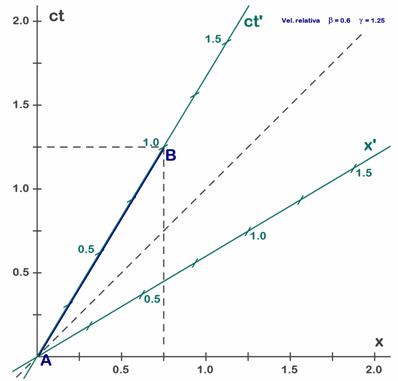
A.5. Ejemplos numéricos y gráficos, 3^a parte

A.5.9.  Ejemplo 5: Dilatación temporal sobre el diagrama de Minkowski.

El segundo problema que nos habíamos planteado era el de entender la dilatación temporal. Es un efecto que sorprende y no es fácil de imaginar, especialmente porque también es simétrico. Veremos de nuevo que la paradoja se debe a que los dos observadores miden tiempos y espacios de manera diferente.

La dilatación temporal se produce al observar un reloj quieto en S’ (o viceversa), y que por tanto desde S se ve en movimiento con el sistema S’.

La línea-mundo de un reloj quieto será una línea paralela al eje de tiempos t’ (verde). En esta línea el valor de la x’ es constante, pero el tiempo t’ varía.

En el gráfico de la Fig. 5.11 hemos escogido observar el reloj que se encuentra en el origen de coordenadas de S’. En el instante inicial se encuentra en A (el origen) y al cabo de 1 segundo se encuentra en el punto de coordenadas (t’=1, x’=0), o sea en B. No se ha movido de x’=0, pero ha pasado un tiempo (1 s) y por esto se desplaza en el eje de tiempos.

Fig. 5.11 -  Dilatación temporal: unidad temporal de S’ vista desde S.

Los sucesos A (pasar por el origen) y B (pasar por el  punto B(x’=0, t’=1)) representan el principio y el final de un proceso que hemos dibujado como una línea azul por similitud con lo que hacíamos en los apartados anteriores, aunque la medida de tiempos no se parece mucho a la de longitudes.

Visto desde S’ el tiempo transcurrido entre los dos sucesos es de 1 unidad (si usamos “ct” deberíamos usar el metro-tiempo), y sobre este hecho no hay ninguna duda ya que los dos hechos los ve el mismo observador y los mide con el mismo reloj (en S’). La barra azul citada coincide con este intervalo de tiempo y podemos decir que materializa esta unidad de tiempo para S’.

¿Cómo verán el paso del tiempo desde S?

Observemos que para S el reloj no ha estado quieto, sino que se ha desplazado hasta la posición x=0,75. Aunque los observadores de S pueden leer el reloj de S’, este no marca un tiempo correcto para los observadores de S. Deberemos leer el tiempo que marcan los relojes de S para el suceso B.

¿En que instante ocurre para S el suceso B?

Para ver la posición hemos trazado la línea de lectura vertical desde el punto B al eje x (negro). Análogamente para ver el tiempo trazamos por B una horizontal (paralela al eje de espacios negro). Esta línea de lectura corta en 1,25, indicando que para S han transcurrido 1,25 unidades de tiempo.

Es importante tener en cuenta que la medida de tiempos la hace un observador de S que se encuentra junto a B (podemos decir que en B) en ese momento, y que hemos dicho que es capaz de ver la hora que marca el reloj de S’ que pasa a su lado en ese momento. Este observador ve en su reloj 1,25 s, mientras que en el de S’ que tiene a su lado ve 1 s. Está claro que los dos sistemas no miden igual los tiempos.

Los observadores de S se fían del observador que estaba en el punto B, pues saben que este tiene el reloj sincronizado con todos ellos. No pueden leer tiempos en un solo reloj porque el objeto se ha movido. Basan sus medidas en la confianza en sus observadores y el concepto de sincronización.

En cambio el reloj de S’ que se ha movido de A a B es el mismo reloj que un rato antes pasaba por el origen (suceso A). Al ver que ese reloj de S’ marca menos tiempo del que marcan sus propios relojes no les cabe ninguna duda de que el tiempo de S’ transcurre más despacio.

Esto resulta sin duda sorprendente, y podríamos intentar encontrar alguna explicación (como hacíamos en el apartado A.5.1). Pero lo paradójico no es que para S parezca que los relojes de S’ van más lentos sino que si miramos S desde S’ debe ocurrir lo mismo (no existen sistemas de referencia privilegiados) y por tanto para S’ son los relojes de S los que se ven más lentos. Lo veremos en el siguiente apartado.

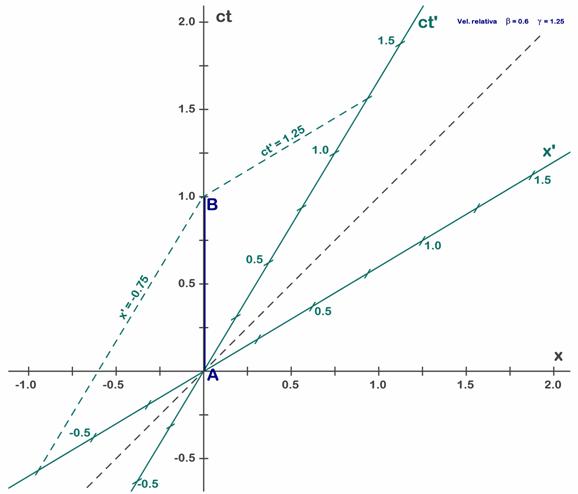
A.5.10.  Ejemplo 6: Dilatación temporal inversa sobre el diagrama de Minkowski.

La dilatación temporal vista desde S’es similar, pero resulta más difícil de ver porque ahora se ve el reloj de S que se aleja del origen de S’ en dirección contraria.

La dificultad reside en que no hemos dedicado tiempo a explicar como utilizar los diagramas en dirección contraria y no vale la pena dedicarle mucho tiempo porque no volveremos a usarlos, así que haremos las indicaciones necesarias para poder interpretar el gráfico, pero no nos extenderemos demasiado en los comentarios, que por otro lado son semejantes a los de los apartados anteriores.

Ahora el segmento azul AB representa un intervalo temporal de 1 unidad observado sobre un reloj inmóvil de S (permanece en x=0 todo el tiempo). Visto desde S’ el reloj se mueve con el origen de S

Para ver como ven desde S’ el suceso B trazamos las paralelas a sus ejes. La paralela al eje x’ (verde) pone de manifiesto que t’=1,25, mientras que la paralela a eje temporal t’ (verde) nos da que x’= – 0,75. Este resultado es idéntico al obtenido en el apartado anterior, excepto el signo negativo de x’, que es debido a que ahora estamos mirando desde S’ y vemos como S se aleja en sentido contrario.

Fig. 5.12 -  Dilatación temporal inversa: unidad de S vista desde S’.

Si comparamos el tiempo visto desde S’ y el leído en el reloj de S veremos una situación simétrica a la del apartado anterior. Vemos 1 s en el reloj de S mientras nuestro reloj (de S’) marca 1,25 s. .

Los diagramas de Minkowski vuelven a poner en evidencia que la aparente paradoja se debe a que en los dos casos (Fig. 5.11 y Fig. 5.12) miramos objetos distintos (en un caso miramos un reloj de S y en el otro uno de S’) desde dos sistemas que usan maneras diferentes de medir.

La conclusión es que no se puede afirmar que un tiempo vaya más rápido que otro, pues eso depende de quien lo mire. Siendo más precisos deberíamos decir que depende de quien lo mira y del objeto que mira, ya que en nuestro caso la diferencia residía en mirar un reloj de S o uno de S’.

Una vez más vemos que ambos sistemas usan escalas de tiempo distintas y no comparables (una no es mayor ni menor que la otra) más que para sucesos concretos. En el siguiente apartado veremos que para sucesos concretos el intervalo de tiempo queda perfectamente determinado y en general las medidas de ambos serán distintas.

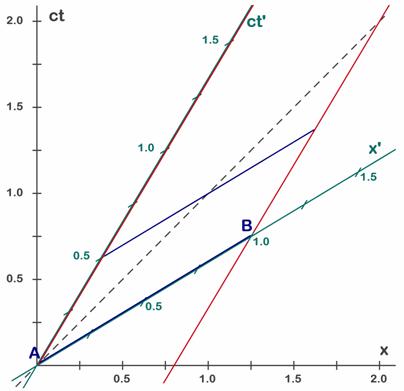
A.5.11.  Sobre la mezcla de longitudes y tiempos.

Otra forma de ver que los sistemas siguen escalas espaciales y temporales independientes es observar que lo que para un sistema es tiempo para el otro puede ser espacio. La mezcla de ambos no es perfecta, no puede hacerse de cualquier forma, pero sin duda se mezclan.

En el ejemplo de la dilatación temporal hemos visto que el reloj de S’ no se mueve de su origen, con lo cual este reloj (barra azul de la Fig. 5.11, que mide 1 s) sólo sufre cambios en la coordenada temporal, pero mantiene constante la coordenada espacial. Se dice que la distancia que separa ambos sucesos es temporal, en este caso es una distancia temporal pura.

Sin embargo al mirarlo desde S varían tanto la coordenada temporal como la espacial (1,25 s  y 0,75 sl). La evolución de este objeto se ve compuesta de evolución temporal y espacial.

En el ejemplo de la contracción de longitudes (Fig. 5.7) ocurre justo lo contrario pero no es fácil de ver porque usamos una barra con dos extremos, ambos en movimiento, y no necesitamos mantener constante la variable temporal porque la rigidez del sólido mantiene la longitud a lo largo del tiempo.

Repetimos a continuación aquel diagrama y consideremos dos sucesos simultáneos para S’ que llamamos A y B. El suceso A ocurre en el instante t’=0 en la posición x’=0, mientras el suceso B ocurre en el mismo momento t’=0 pero en x’=1.

Fig. 5.13 -  Sucesos simultáneos en S’ no lo son en S.

La situación es la misma que estudiábamos en el ejemplo 3 sobre contracción de longitudes.

Visto desde S’ la separación entre ambos sucesos es puramente espacial, ya que la simultaneidad significa distancia temporal nula. Se dice que les separa una distancia espacial pura.

Sin embargo visto desde S la separación espacial cambia y aparece una separación temporal. La distancia temporal medida desde S es de 1,25 s y la distancia espacial de  0,75 sl.

La distancia entre los dos sucesos se ve compuesta de parte temporal y parte espacial.

Sin duda la estructura del espacio-tiempo mezcla de formas diferentes (en proporciones diferentes) el espacio y el tiempo según el sistema de referencia que haga las medidas.

En el próximo capítulo discutiremos un poco más el concepto de simultaneidad y el de causalidad, clasificando los sucesos según que se puedan o no relacionar mediante estos conceptos.

A.5.12.  Conclusiones.

Los ejemplos de este capítulo nos han permitido ver que las maneras de medir espacio y tiempo son diferentes según el observador que las haga. Esto es una novedad de la R.E. ya que antes de Einstein se consideraba el tiempo y el espacio como absolutos e inmutables y se creía que todo el mundo tenía que verlos y medirlos igual.

Esta diferente manera de medir da lugar a situaciones paradójicas que chocan con nuestra experiencia cotidiana y a mucha gente les hace dudar de la validez de la Relatividad, sin embargo hay que tener en cuenta que la propia R.E. ya prevé que la mayoría de estos efectos serán difíciles de observar.

En el apartado A.4.8 hacíamos hincapié en que los efectos relativistas sólo se podían notar a grandes velocidades. Concluíamos que

Estos dos efectos son los más notables y los que chocan más directamente con nuestra intuición.

Con las novelas y películas de ciencia-ficción ya nos hemos hecho a la idea de que pueda jugarse con el tiempo y estamos mas dispuestos a aceptar que el tiempo transcurra a otro ritmo para otros sistemas, e incluso que se pueda viajar en el tiempo (cosa que la Relatividad Especial no prevé).

Sin embargo la contracción de longitudes siempre se ha comprobado indirectamente y nunca será fácil de comprobar. Concluíamos que

En los capítulos siguientes estudiaremos algunos de los problemas más famosos que ha generado la Relatividad. En ellos pondremos a prueba a fondo las capacidades de los diagramas de Minkowski que hemos estudiado en este capítulo.