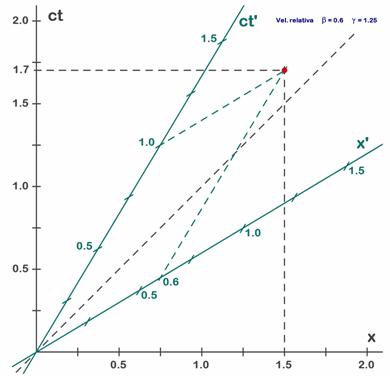
A.5. Ejemplos numéricos y gráficos, 2^a parte

A.5.5.  Ejemplo 1: Lectura de puntos sobre un diagrama de Minkowski.

Los diagramas de Minkowski ponen en evidencia lo que se ve desde cada uno de los sistemas de coordenadas, y esto resulta muy ilustrativo para entender las paradojas de la relatividad.

Como primer ejemplo del uso de los diagramas podemos mirar como se ve un mismo suceso desde ambos sistemas de coordenadas (un punto o par de coordenadas del espacio-tiempo).

En la figura 5.6 podemos ver que el punto rojo que en S tiene coordenadas (ct=1,7  x=1,5) se ve en S’como (ct’=1,0  x’=0,6).

Obsérvese que para leer las coordenadas negras trazamos líneas verticales y horizontales, mientras que para leer las coordenadas verdes trazamos líneas oblicuas. En ambos casos las líneas que trazamos, que llamaremos líneas de lectura, son paralelas a los ejes de ese color. Las líneas de lectura verdes son paralelas a los ejes verdes y las negras son paralelas a los ejes negros.

Aunque aquí no podemos extendernos explicando técnicas de dibujo, indicaremos que si dibujamos a mano, para obtener un resultado aceptable hay que trazar las paralelas con escuadra y cartabón. Una alternativa mejor es el uso de programas de dibujo dentro del ordenador, pero estos programas requieren horas de dedicación. Si os interesa este tema podréis encontrar manuales y cursos en internet con los que iniciaros en diversos programas de CAD, de dibujo vectorial (inkspace), de geometría o de dibujo en general (gimp).

Volviendo a los diagramas de Minkowsky, veamos como se pueden utilizar para aplicar la transformación de Lorentz a cambiar de un sistema a otro.

Fig. 5.6 -  Representación de la transformación

de Lorentz (lectura de coordenadas en S y S’).

Si por ejemplo nos dan las coordenadas en el sistema S (ct=1,7  x=1,5) podemos trazar las líneas de lectura para encontrar el punto que representan (el punto rojo de la Fig. 5.6) y después si trazamos las líneas de lectura verdes (paralelas a los ejes verdes) a partir del punto rojo que hemos obtenido antes, podremos leer las coordenadas en el sistema verde S’como (ct’=1,0  x’=0,6).

Si nos dan coordenadas de S’ el proceso será a la inversa, pues deberemos comenzar por dibujar las líneas de lectura verdes y obtener el punto rojo para después leer en los ejes negros.

La única limitación de estos diagramas radica en que si trazamos muchas líneas sobre un mismo gráfico este pierde su efectividad para aclarar ideas. Como veremos en los ejemplos siguientes, resulta más efectivo realizar dos gráficos similares que uno con muchas líneas.

Una vez sabemos leer los diagramas de Minkowski ya estamos en condiciones de utilizar estos diagramas para resolver problemas de R.E.. El primer problema que nos planteamos es el de aclarar el significado de la contracción de longitudes y la dilatación de tiempos. Antes conviene introducir el concepto de línea-mundo o línea de evolución en el tiempo.

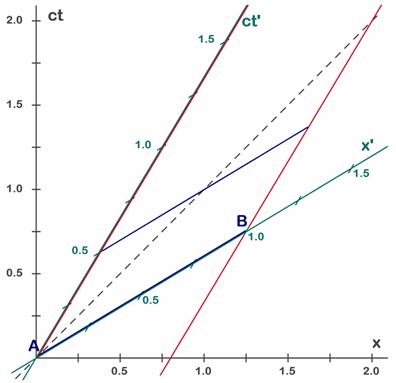
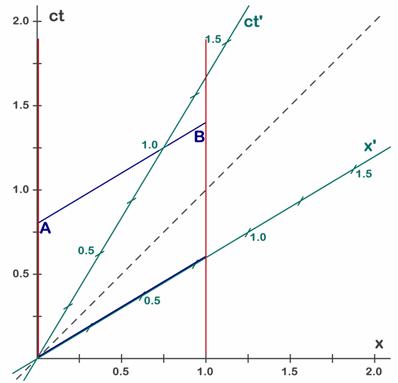
A.5.6.  Ejemplo 2: Línea de evolución de objetos quietos y en movimiento.

Consideremos una barra que mida un metro en reposo, y que S’ se lleva en su viaje como patrón de longitudes. Supongamos para simplificar que lo colocan con un extremo (A) sobre su origen de coordenadas (x’=0) y el otro a un metro de distancia en la dirección de su eje x (x’=1) y supongamos que nunca lo mueven de allí.

Hemos dibujado la posición inicial de la barra en ct’=0 como una línea azul (Fig. 5.7) sobre el eje de las x’ (eje verde).

A pesar del paso del tiempo (ct’=0, 1, 2, ...) la posición del extremo A siempre es x’=0, lo cual significa que la línea que representa su evolución temporal en el diagrama espacio-tiempo será una recta que está sobre el eje de tiempos (coincide con el eje de tiempos) ya que el eje de tiempos (verde) corresponde a todos los puntos con  x’=0.

Hemos dibujado en rojo sobre el eje verde ct’ la línea-mundo o línea evolutiva del extremo izquierdo (A). Análogamente el extremo derecho B tiene una evolución temporal o línea-mundo paralela a la anterior (línea roja derecha) y que pasa por la abcisa x’=1, que es la posición inicial elegida para este lateral.

Con el paso del tiempo (ct’=0, 1, 2, ...) la posición del extremo B siempre es x’=1, lo cual significa que la línea que representa su evolución temporal en el diagrama espacio-tiempo será una recta paralela a la anterior que pasa por x’=1. Es la línea roja de la derecha.

Cualquier línea paralela al eje de tiempos representa un objeto inmóvil que evoluciona en el tiempo. Para varios instantes de tiempo (t cambia) vemos que la posición (x’) no cambia.

Visto desde S la línea roja no es paralela al eje de tiempos (de S) y por tanto representa un objeto en movimiento, en este caso el extremo derecho de la barra (B) que se mueve con el sistema S’.

Entre los objetos importantes conviene observar que la línea roja izquierda, que coincide con el propio eje de tiempos de S’, representa el movimiento de un objeto (A) situado siempre en el origen de coordenadas de S’. En consecuencia la línea de tiempos representa el movimiento del propio origen de S’ (el punto que tiene siempre x’=0) respecto a S.

A.5.7.  Ejemplo 3: Contracción de longitudes sobre el diagrama de Minkowski.

Consideremos la barra del ejemplo anterior. Mide un metro (en reposo) y  S’ lo lleva en su viaje como patrón de longitudes. Hemos supuesto que lo colocan con un extremo (A) sobre su origen de coordenadas (x’=0) y el otro a un metro de distancia en la dirección de su eje x (x’=1) y que nunca lo mueven de allí. La posición inicial de la barra en ct’=0 está representada la figura 5.7 como una línea azul sobre el eje de las x’ (sobre el eje verde horizontal).

Como ya hemos dicho, a pesar del paso del tiempo (ct’=0, 1, 2, ...) la posición del extremo A siempre es x’=0. Su línea-mundo será la recta roja que está sobre el eje de tiempos (coincide con el eje de tiempos verde) y corresponde a todos los puntos con  x’=0.

Análogamente el extremo B tiene una evolución temporal o línea-mundo paralela a la anterior y que pasa por la abcisa x’=1. Es la línea roja de la derecha.

Fig. 5.7 -  La longitud de la barra vista desde S’ siempre es 1m.

De una posición a otra lo único que cambia es el tiempo.

Es importante observar que en el sistema S’ miran la posición de la barra observando sus dos extremos en un mismo instante de tiempo, y para ello en el diagrama usamos líneas paralelas a su eje de espacios (paralela al eje verde x’).

Las dos líneas azules representan como se ve la barra en S’ en dos instantes diferentes. La barra inferior está sobre el eje x’ y por tanto todos sus puntos se encuentran en el instante t=0. Es la representación de la barra en su posición de partida en el instante t=0. La barra superior (ambas barras aparecen inclinadas) tiene todos sus puntos en el instante  t=0,5 (todos sobre una paralela al eje x’) y por tanto representa la posición de la barra en ese instante.

El hecho de que vean la barra inclinada es propio del sistema S’, pues es su manera de ver la simultaneidad. Las cosas que ocurren en el mismo instante siempre caen sobre la misma paralela al eje x’ (verde).

Obsérvese también que para S’ la barra siempre medirá 1 m. El extremo izquierdo A de la barra está siempre sobre la línea roja izquierda (el cero de longitudes en S’) y el extremo derecho B siempre sobre la línea roja derecha (el 1 de longitudes de S’).

Evidentemente en el sistema S (negro) no medirán las cosas de la misma manera.

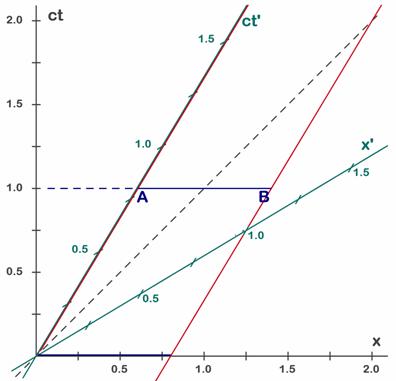
¿Cómo ven la barra de 1 metro desde S?

En el sistema S también miran la posición de la barra mirando sus dos extremos en un mismo instante de tiempo, pero ahora hay que usar paralelas a los ejes negros, que son los de S.

En la Fig. 5.8 hemos dibujado dos posiciones de la barra (en azul) tal como la ven desde S. En el instante inicial t=0 ven el extremo A sobre el origen, pues en este instante ambos orígenes coinciden. Como este extremo está en t=0 hay que mirar donde ven los demás puntos en ese mismo momento t=0. Evidentemente ahora los puntos están en el mismo instante de tiempo si están en una recta horizontal, en este primer momento esta recta es el propio eje x (negro), por esto la posición inicial que ven en S para la barra es la línea azul de abajo, sobre el eje x. 

Fig. 5.8 -  La longitud de la barra vista desde S siempre es 0,8m.

En la Fig.5.8 hemos dibujado una segunda posición que corresponde a t = 1. Para mirar todos los puntos en el mismo instante de tiempo deberemos mirar en una línea horizontal, paralela al eje x negro. La representación de la barra en el instante t=1 es la línea azul  de arriba (Fig. 5.8).

Está claro que la medida será menor que uno. Si miramos la posición del extremo B (trazando la línea de lectura vertical) veremos que en el instante t=1 está en x=1,4, mientras que el extremo A está en x=0,6. Esto da una longitud de 0,8 metros (abreviaremos escribiendo 0,8 m).

Aun más fácil es verlo en la posición inicial, o sea mirando la barra azul de abajo. En el instante t=0 un extremo está en el origen (x=0) y el otro en x=0,8, por tanto esta es la longitud de la barra.

Igual que ocurría en S’, la longitud mide siempre lo mismo, pero debido a la diferente forma de medir (uno con líneas oblicuas y el otro con líneas horizontales) en un sistema siempre mide 1 m y en el otro siempre 0,8 m.

Luego evidentemente desde S se ve la contracción de longitudes que esperábamos.

La discrepancia entre la medida en un sistema y en otro se debe a que ven evolucionar el tiempo de forma distinta. Vemos que la medida de objetos extensos obliga a mirar los extremos simultáneamente y en los dos sistemas la simultaneidad se ve de forma diferente.

A.5.8.  Ejemplo 4: Contracción inversa de longitudes sobre el diagrama de Minkowski.

La primera paradoja que citábamos consiste en que desde S’ también verán encogerse las unidades de S.

Ya hemos comentado que aunque parece imposible es así, y lo interesante de los diagramas de Minkowski es que permiten entender lo que esto significa.

La diferencia más importante es que ahora la barra de un metro estará en S y por tanto para S está en reposo y su longitud es la del reposo: un metro.

Suponemos para simplificar que se coloca el extremo izquierdo sobre el origen de coordenadas (x=0) y el derecho a un metro de distancia en la dirección de su eje x (x=1) y suponemos que nunca los mueven de allí.

A pesar del paso del tiempo (ct=0, 1, 2, ...) la posición del extremo izquierdo siempre es x=0, lo cual significa que la línea-mundo o línea evolutiva del extremo A estará siempre sobre el eje de tiempos ya que esta es la representación de los puntos que tienen  x=0.

Fig. 5.9 -  La longitud de la barra vista desde S siempre es 1m.

En el gráfico de la Fig. 5.9 hemos dibujado en rojo sobre el eje negro ct la línea-mundo o línea evolutiva del extremo A. El extremo B tiene una evolución temporal o línea-mundo paralela a la anterior y que pasa por x=1, que es la posición inicial elegida. La línea-mundo del extremo B es la línea roja de la derecha.

Como en S miran la posición de la barra mirando sus dos extremos en un mismo instante de tiempo, en el diagrama usaremos líneas paralelas a su eje de espacios (eje x negro).

En la Fig. 5.9 hemos dibujado la posición de la barra en t=0 (barra azul de abajo) y en t=1 (barra azul de arriba).

Observamos que para S la barra siempre medirá 1 m.

¿Y como se ve desde S’?

Para saber como lo verá S’ debemos mirar los dos extremos en un mismo instante de tiempo t’, lo cual significa usar paralelas a su eje de espacios x’ (verde).

Las líneas-mundo de los extremos no cambian, siguen siendo las líneas rojas, pero la manera de elegir los puntos simultáneos cambia, y la medida obtenida también cambiará..

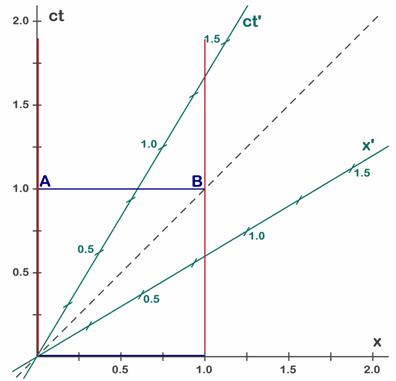
Fig. 5.10 -  La longitud de la barra vista desde S’ siempre es 0,8m.

En la figura 5.10 podemos ver que al usar paralelas al eje x’ (verde) para medir la longitud resulta que la representación de la barra viene dada por las líneas azules oblicuas y la longitud (medida sobre el eje verde horizontal) es de 0,8 m. Es más, para S’ la barra siempre medirá 0,8 m (ambas barras azules y todas las que queramos dibujar).

Vemos pues una situación totalmente simétrica de la que teníamos en el apartado anterior. Ahora S’ ve la barra de S en movimiento y ve como se contrae.

Aunque resulte chocante, sobre los diagramas está claro que todo cuadra. S ve encoger el metro de S’ y S’ ve encoger el metro de S.

Está claro que medimos objetos distintos (en el primer caso el metro viaja con S’, mientras que en el segundo caso permanece con S) y usamos patrones de tiempo distintos para considerar simultáneas dos cosas. Esto es lo que genera la paradoja (una contradicción aparente).

Pero es importante ver que los diagramas de Minkowski nos han servido para algo más, pues en ellos vemos que la discrepancia (entre la medida en un sistema y en el otro) es debida a como ven cada uno de ellos la simultaneidad.