A.5. Ejemplos numéricos y gráficos

A.5.1.  Sistemas inerciales simétricos.

Para concretar nuestros dos sistemas inerciales imaginaremos dos trenes muy largos uno al lado del otro, de manera que cada observador podrá ver lo que ocurre en la parte del otro tren que está pasando a su lado, aunque si fuera un tren real pasaría a tanta velocidad que nos costaría ver algo. Entre otras cosas supondremos que en cualquier momento ve un observador del otro tren pasando a su lado. Supondremos que puede leer la posición de ese observador dentro del otro tren y que puede ver la hora el reloj que lleva ese otro observador.

Cuando ocurra algún suceso (como el paso de un observador o una explosión) el observador tiene la función de informar a sus compañeros de tren de la hora y posición reales (las que ve en su propio reloj y en su propia cinta métrica) del suceso y de la hora y posición que ve en S’ (datos del otro tren).

El tren deberá ser muy largo porque debemos poder hacer experimentos con espacios y tiempos grandes, como el del reloj de luz que medía 300 000 km, así que podemos imaginar que llega hasta los últimos planetas del sistema solar (Urano y Neptuno, pues Plutón ya no se considera planeta) y si hace falta imaginaremos que va más allá.

El origen de coordenadas es el punto en que centralizamos toda la información. A efectos prácticos podemos imaginar que hay un responsable del tren que centraliza la información en una sala de control. Podemos imaginar algo así como el comandante de esa inmensa nave espacial que es nuestro tren. Además supondremos que en el instante inicial de nuestros experimentos ambos comandantes se encuentran uno al lado del otro y que ponen sus relojes a cero. Los relojes de la primera nave S están todos sincronizados con el del primer comandante y los relojes de la segunda nave S’ están todos sincronizados con el del segundo comandante. 

Nuestro problema fundamental es entender como se realizan las medidas, y con frecuencia estas nos conducen a situaciones paradójicas como la siguiente. Hemos dicho que en el instante inicial los relojes de ambos comandantes se ponen a cero (se sincronizan). Los relojes de la primera nave S están todos sincronizados con el del primer comandante y los relojes de la segunda nave S’ están todos sincronizados con el del segundo comandante. A primera vista da la sensación de que en ese instante inicial todos los relojes de todos los observadores de S deben coincidir con los de sus homólogos de S’, pero no es así, pues miden los tiempos y la simultaneidad de formas diferentes.

También da la sensación de que es una situación muy simétrica y que las longitudes inicialmente deben medirse igual, es decir, que el observador que está a 100 metros del comandante de la primera nave debe tener a su lado al observador que el segundo comandante tiene a 100 metros, pero tampoco es así, pues también miden las distancias de maneras diferentes.

Si queremos aclarar estas paradojas necesitamos un instrumento que nos permita razonar con una precisión aceptable, y este instrumento son los diagramas de Minkowski a los que dedicamos este capítulo.

Tener las ecuaciones de Lorentz no nos aclararía más las cosas, e incluso con ellas deberíamos razonar sobre diagramas espacio-tiempo. Los problemas más interesantes de la R.E. se pueden estudiar con mucho detalle sobre estos diagramas sin necesitar nunca ninguna ecuación.

A.5.2.  Las unidades de espacio-tiempo: el segundo-luz y el metro-tiempo.

Al utilizar las transformaciones de Lorentz veremos que en R.E. el espacio y el tiempo se mezclan íntimamente, hasta el punto de que lo que en un sistema es espacio en otro puede ser tiempo. Esto nos lleva a revisar las unidades que utilizamos para longitudes y tiempos.

En astronomía es usual utilizar el año-luz (que se suele abreviar “al”) para medir grandes distancias ya que las unidades que nos son más familiares (metro, kilómetro,...) se quedan muy cortas. Es la distancia que recorre la luz en un año y es una distancia de casi diez billones de kilómetros (9,46 billones de km).

Nos interesa entender este ejemplo porque es un caso real en el que se usa el tiempo para medir distancias.

Si nos dicen que Próxima Centauri (la estrella más próxima a nosotros después del Sol) está a 4,27 años-luz de distancia, realmente nos están dando el tiempo que tarda su luz en recorrer la distancia hasta nosotros (4,27 años). Aunque esto puede sorprender, en realidad es una unidad que nos permite apoyarnos en conceptos muy intuitivos para hacernos una imagen de las dimensiones estelares: la velocidad de la luz y la idea de larguísimos viajes interestelares.

Como sabemos lo que es un año-luz podríamos pasar este tiempo (4,27 años) a kilómetros sin mucho esfuerzo. Sin embargo esto no nos aclararía nada y el número resultante resultaría muy  grande y engorroso de manejar. En la práctica es más sencillo hablar de 4,27 años luz.

En R.E. esa distancia es, en muchos casos, demasiado grande, así que frecuentemente usaremos el segundo-luz.

El segundo-luz (que podemos abreviar “sl”) es la distancia recorrida por la luz en un segundo (unos 300 000 km). Es una distancia que se utiliza con frecuencia en R.E. y nosotros lo hemos hecho al describir nuestro reloj de luz (apartado A.4.1) y nuestro interferómetro (apartado A.4.3).

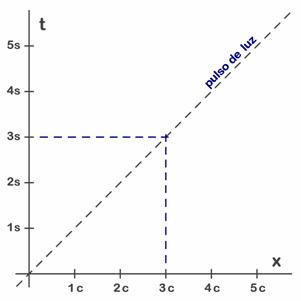
Aunque “c” es una velocidad, en R.E. es frecuente hablar de “una distancia c” y nosotros ya lo hemos hecho en varias ocasiones. Así lo hacen casi todos los textos de R.E. y su uso para indicar distancias está tan extendido que en la práctica no tiene sentido usar el sl (que sería la unidad correcta).

Sin embargo conviene aclarar que a veces se usa como unidad, en cuyo caso significa lo mismo que el sl, mientras que en otras ocasiones se utiliza como un número (c = 300 000) y este doble uso puede generar confusiones ¿qué significa en la figura 5.1?

En la figura 5.1 se puede ver el uso habitual de estas unidades en los diagramas espacio-tiempo.

Como curiosidad (ya que en este curso de nivel introductorio no hacemos cálculos) diremos que igual que hemos usado una unidad de tiempo para indicar distancias podríamos usar distancias para indicar tiempos, cosa muy frecuente en relatividad.

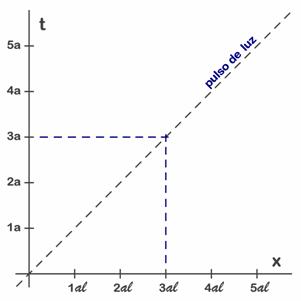
Esta unidad de tiempo es muy pequeña (1/300 000 000 s) y se utiliza cuando interesa utilizar metros en el eje de espacios, pues en los diagramas de Minkowski siempre se procura que ambas unidades sean del mismo orden, de manera que un rayo de luz siempre siga la dirección de la diagonal principal (Fig. 5.1, 5.2, 5.3 y 5.4). Cuando se indica “ct” en el eje de tiempos significa que se usan estas unidades (véase la Fig. 5.5 y sus comentarios en el texto).

No está de más observar que el interés de estas parejas de unidades reside en que en la R.E. el tiempo y el espacio se mezclan y funden entre si. Veremos que en cierta manera lo que para un observador es tiempo para el otro es espacio.

También es interesante observar que detrás de estos conceptos siempre está la luz y la velocidad de la luz. Para crear un buen diagrama resultará imprescindible que siempre quede claro como se representa el movimiento de un rayo de luz. En las figuras 5.1 y 5.2 la línea oblicua representa el movimiento de un pulso de luz a lo largo del tiempo. Obsérvese que al cabo de 1s ha recorrido un espacio “c”, al cabo de 3s un espacio 3c (señalado en azul), etc.

Para entender la R.E. y las transformaciones de Lorentz es imprescindible entender que la simultaneidad (mismo instante) y la equilocalidad (mismo lugar) no se ven igual desde un sistema y desde el otro, y para esto necesitamos saber utilizar estos diagramas espacio-tiempo.

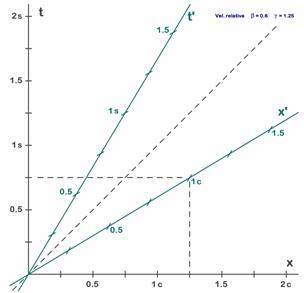
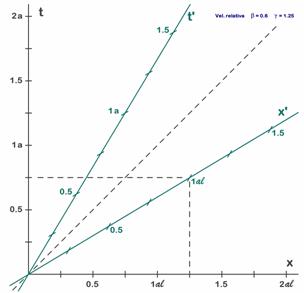
A.5.3.  Diagramas espacio-tiempo (de Minkowski):

Los diagramas espacio-tiempo se utilizan para relacionar dos sistemas, el S del observador de tierra firme y el S’ del observador del tren en movimiento.

El primer sistema de referencia será el S del observador de tierra firme y lo representaremos en tinta negra, como en las figuras 5.1 y 5.2.

El segundo sistema será el S’ del tren y lo representaremos siempre en verde, superponiéndolo al anterior, por lo que nuestros diagramas siempre tendrán cuatro ejes.

La costumbre en Relatividad es utilizar el eje horizontal para representar espacios (va marcado con la letra x o con x’) y el vertical para tiempos (marcándolo con t o con t’).

En la mayoría de casos utilizaremos las unidades de las figuras 5.1 y 5.3, o sea segundo y segundo luz (aunque escribiremos c en lugar de sl), pues los movimientos que estudiaremos durarán un segundo o dos (como en los ejemplos de los capítulos anteriores).

Cuando estudiemos los viajes espaciales y el problema de los gemelos necesitaremos utilizar unidades mucho mayores y cambiaremos las unidades por el año y el año-luz (figuras 5.2 y 5.4).

¿Para qué sirven estos diagramas?

Estos diagramas fueron propuestos por Minkowski y resultaron múy útiles para interpretar los resultados obtenidos con las ecuaciones de Lorentz. Podríamos decir que nos permiten obtener una imagen geométrica (visible) del nuevo concepto de espacio y tiempo que introduce la R.E.

En los apartados siguientes veremos que estos diagramas permiten obtener resultados numéricos muy precisos sin hacer un sólo cálculo. En lugar de fórmulas y calculadora usaremos lápiz y regla.

En caso de encontrar dificultades para interpretar los diagramas, en el apéndice 1 se pueden encontrar aclaraciones adicionales.

A.5.4.  Calibrar el segundo sistema de referencia (S’):

Para representar correctamente el segundo sistema de referencia (a esta operación le llamaremos “calibrar”) bastará aplicar las transformaciones de Lorentz a las unidades de espacio y tiempo.

Tomaremos la velocidad del sistema S’ (necesitamos la velocidad del tren o de la nave para poder preparar el diagrama) y miraremos en la tabla 1 que contracción espacial y que dilatación temporal corresponde a esta velocidad, o sea, leeremos el factor gamma que le corresponde.

Para muchos ejemplos utilizaremos una velocidad de 0,6 c (0,6 veces la velocidad de la luz) o lo que es lo mismo, 180 000 km/s. Este valor aparece en la tabla 1 y lo hemos elegido porque es el que permite hacer diagramas más sencillos.

Dibujaremos estos nuevos ejes en verde y aceptaremos que tienen una inclinación o pendiente de 0,6. Esto significa que sobre el uno negro hay que marcar un punto verde a una altura de 0,6 y sobre el 2 negro un punto verde a una altura del doble (1,2). Esto permite dibujar el eje de espacios verde (x’). El eje de tiempos se dibuja exactamente igual pero girando el papel.

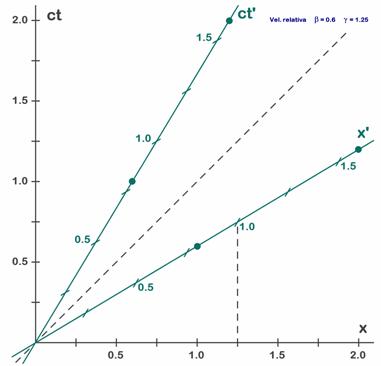
Fig. 5.5 -  Representación de los ejes de S’

debidamente calibrados para .

Para calibrar el diagrama, o sea para marcar las unidades verdes usaremos el factor gamma.

Sabemos que el tiempo del tren pasará 1,25 veces más lento y sus longitudes se contraerán con un factor 1,25. Dicho de otra forma, las unidades de longitud o espaciales (x) del sistema S (el observador en tierra firme) serán 1,25 veces mayores que las del tren, y las temporales también.

Esto significa que donde en los ejes de S (en negro) marca 1,25 unidades, en el eje de S’ (en verde) deberá marcar sólo 1 unidad. En la figura 5.5 se puede ver como calibrar el eje verde de espacios. El trazo vertical sobre 1,25 nos sirve para situar la unidad verde o de S’. El de tiempos se calibra exactamente igual aunque no lo hemos dibujado.

Observamos que el diagrama es simétrico y es que para las transformaciones de Lorentz el espacio y el tiempo funcionan exactamente igual.

Conviene trazar la bisectriz del cuadrante, ya que como hemos visto al comentar las figuras 5.1 y 5.2, esta línea representa la evolución temporal de un rayo de luz (sería más correcto decir un pulso de luz) y nos sirve de referencia para las demás líneas que trazaremos, que casi siempre serán simétricas respecto a esta línea de luz.

Una vez situados los puntos unitarios ya podemos representar los ejes de S’ con tantas divisiones como queramos y comenzar a utilizar el diagrama de Minkowski para estudiar problemas.

En el diagrama de la figura 5.5 y en muchos de los que usaremos veremos que no se indican unidades. El motivo es que funciona igual si son segundos y segundos-luz (como en la Fig. 5.1) o son años y años‑luz (como en la Fig. 5.2).

Realmente si el eje de tiempos está indicado como “ct” (que es lo habitual en Relatividad) significa que se usa la unidad natural: metro y metro-tiempo. Aun así con frecuencia se escribe “c” en uno o en ambos ejes, queriendo indicar lo mismo que en los diagramas 5.1 y 5.3.

Pero dado que los tres tipos de unidades funcionan bien, podemos interpretar el gráfico indistintamente con cualquiera de las tres parejas de unidades: con metro y metro-tiempo, con segundo-luz (c) y segundo, o con año-luz y año.