A.4. Las transformaciones de Lorentz, 3^a parte (nivel A).

A.4.7.  La contracción de longitudes (o contracción de Lorentz).

Está claro que la única manera de que el pulso horizontal alcance el espejo de la derecha antes de completar el segundo medio ciclo es que su longitud se haya acortado más del 18 % (que es lo que le falta según nuestro cálculo anterior). Repasemos las medidas que hemos encontrado para ambos observadores.

Si ambos tubos medían “c”, para el observador del tren la luz tarda un segundo para llegar arriba, mientras que tarda 1,41 segundos para el observador de tierra firme (como se puede comprobar en la cinta métrica del dibujo, pues recorre una longitud 1,41 veces mayor). Este hecho no nos extraña pues ya sabíamos que el tiempo pasa más lento para el observador en movimiento. 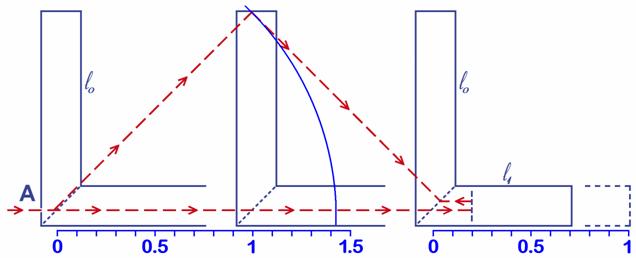Éste número será además el factor gamma () (véase el apartado A.4.2 y la tabla 1).

Para el observador del tren el pulso del tubo horizontal también tarda un segundo en llegar al fondo del tubo, pues ambas longitudes son iguales y la velocidad de la luz es la misma en todas direcciones.

Sin embargo para el observador de tierra firme el pulso del tubo horizontal tiene un recorrido muy asimétrico (Fig. 4.4 y 4.5). Tras medio ciclo (tras 1,41 segundos) sólo ha recorrido un 41 % de la longitud del tubo original y si este no se contrajera no podría terminar de recorrerlo en el otro medio ciclo (otros 1,41 s).

Para el observador de tierra firme el pulso vertical tardará otros 1,41 segundos en regresar al espejo de abajo, pues el recorrido de este pulso es perfectamente simétrico. Durante esta segunda fase del viaje el pulso horizontal debe llegar al extremo del tubo y regresar, pero no podrá llegar al otro extremo a menos que esté a menos de otras 0,41 unidades y esto exige que el tubo horizontal se haya contraído.

Fig. 4.9 -  Si el tubo horizontal no se encoge el pulso horizontal no puede llegar a tiempo.

La situación real se puede ver en la figura 4.8. Hemos dibujado el brazo horizontal mucho más corto, pero no es ninguna exageración, es la longitud que necesita tener el brazo horizontal para que la luz tenga tiempo de llegar al espejo de la derecha y regresar al de la izquierda a tiempo.

La contracción detectada resulta tener el mismo factor gamma que aparecía en la dilatación de tiempos. La longitud del brazo se ha acortado en un factor de 0,71 (mide un 71% de lo que medía, o sea de lo que mide el tubo vertical), que equivale a que el brazo más largo (el vertical) sea 1,41 veces mayor que el pequeño.

La velocidad que lleva el tren (y el interferómetro) es fácil de calcular dividiendo el espacio recorrido (c = 300 000 km) y el tiempo que ha tardado (1,41 s), pero también podemos leer en la tabla 1 que la velocidad que corresponde al factor gamma de 1,41 es de unos 210 000 km/s. Esta es la velocidad que lleva el tren y el interferómetro de nuestro ejemplo.

Resumiendo, si ambos observadores ven para la luz la misma velocidad la única explicación posible para esta situación es que los brazos han cambiado de longitud. Si suponemos, igual que cuando estudiábamos el reloj de luz, que el brazo vertical permanece intacto, resulta que el horizontal (que se desplaza en la dirección del movimiento) se habrá contraído en una fracción igual al factor relativista   (su longitud es igual a la original dividida por ese factor; en nuestro ejemplo la longitud queda dividida por 1,41).

A.4.8.  Increíble... pero cierto.

La Relatividad nos ha llevado a dos consecuencias difíciles de admitir:

Haciendo un esfuerzo podríamos imaginar que la velocidad enlentecería los procesos vitales de las personas, como lo hace la hibernación (el frío), o que una imaginaria “presión” debida a esa misma velocidad comprimiría las longitudes, ... pero no es así.

La paradoja reside en que la R.E. afirma que el observador en suelo firme ve como el reloj del tren va más despacio y a la vez que el observador del tren ve el reloj de tierra firme ir más despacio. La Relatividad propone una simetría completa en lo que ven ambos espectadores, pues ninguno de estos sistemas está en reposo. ¡No existen sistemas en reposo!

Aunque en nuestro razonamiento dábamos prioridad al sistema de tierra firme como si estuviera quieto, el Principio de Relatividad (ver el apartado A.3.) afirma que no podemos distinguir sistemas fijos y móviles, pues todas las leyes de la física son iguales en todos ellos, por tanto desde el tren deben ver lo mismo cuando miran a tierra firme.

Ambos hechos se alejan de nuestra experiencia y nos resulta difícil admitir que no haya medidas objetivas para longitudes y tiempos, pero es a lo que nos ha llevado una hipótesis tan sencilla como que todos los observadores ven la misma velocidad para la luz.

Michelson era un gran científico, lo comprobó personalmente varias veces con experimentos muy precisos y sin embargo nunca se lo creyó... así que es bastante normal que nos cueste admitirlo.

En el siguiente apartado analizaremos más a fondo el significado de estas dos afirmaciones.

A.4.9.  La transformación de Lorentz

Lorentz propuso como explicación posible del resultado negativo del experimento de Michelson y Morley que las longitudes debían contraerse en la dirección del movimiento exactamente en la proporción necesaria para compensar el desfase esperado entre los dos recorridos del interferómetro.

Observemos que las relaciones establecidas dejan bien claro que en S’ (el sistema en movimiento) ni el tiempo ni el espacio se miden igual que en S, pero no es fácil entender como es esto. Lo mejor es trabajar algunos ejemplos y ver como toman medidas en ambos sistemas. Así entenderemos porqué ven cosas distintas.

Una de las ideas fundamentales es que cuando hablamos de sistema inercial no nos referimos a un espacio reducido como un laboratorio, sino que es un sistema muy extenso, que se prologa en todas direcciones. Si tenemos que medir distancias importantes directamente (en el instante en que ocurren los sucesos) deberemos tener observadores en los puntos que nos interesen para dar constancia del suceso, de la posición e instante de tiempo en que ocurre.

Nosotros no podemos estar en todas partes a la vez, y no podemos fiarnos de la vista pues los sucesos lejanos no se ven enseguida debido a que la luz (la imagen que debe llegar a nuestra retina) tarda mucho tiempo en llegar. Aunque en la práctica puede resultar inviable, necesitamos observadores en todos los puntos en los que queramos observar lo que sucede (sucesos).

El segundo concepto fundamental en R.E. es el de reloj. El tiempo siempre se ha medido con objetos en movimiento (péndulos, depósitos que se van vaciando, etc.), así que no debe sorprendernos que usemos el movimiento de la luz para medir tiempos. Sin embargo la hipótesis de la constancia de la velocidad de la luz nos ha llevado a ver que

Hemos usado en varias ocasiones el argumento de que si un observador ve que la luz recorre más espacio es que ve pasar más tiempo en su reloj que el otro observador que ve un recorrido menor.

La tercera idea fundamental para entender el significado de la transformación de Lorentz es que

En efecto, la dilatación de tiempos ya se ha comprobado con partículas subatómicas aceleradas a grandes velocidades, con satélites (GPS) que requieren medidas muy precisas de posición y tiempo, y cabe esperar que algún día podremos comprobarlo realizando largos viajes interestelares.

Sin embargo la contracción de longitudes siempre se ha comprobado indirectamente ya que la comprobación directa exigiría medir la longitud de un objeto que se mueve a velocidades muy elevadas respecto a nosotros, y esto siempre será muy difícil de hacer directamente (con una cinta métrica o algo equivalente).

Hay que tener en cuenta que si en el tren llevan una cinta métrica al lado del interferómetro (en posición horizontal) veremos como ésta se acorta igual que el brazo horizontal del interferómetro. Esta medida no es la que ve el observador de tierra firme, pues este debe medir con metros de tierra firme. Una cinta métrica que viaje con el tren medirá lo que ven los propios observadores del tren (S’) y no servirá para apreciar cambios, pues también se contraerá.. Este hecho deja claro que en el sistema en movimiento (dentro del tren) no apreciaran la dilatación temporal ni la contracción de longitudes.

Estas dos transformaciones simétricas, la espacial y la temporal contienen la esencia de las transformaciones de Lorentz, y no necesitaremos ecuaciones para trabajar con ellas, ya que los diagramas de Minkowski reflejan con exactitud las mismas relaciones que las ecuaciones.

Los ejemplos del capítulo siguiente nos servirán para entender mejor estas transformaciones y para despejar las dudas que generan algunas paradojas como la de la simetría. Veremos que esencialmente todo se reduce a que cada sistema mide de manera diferente.