A.4. Las transformaciones de Lorentz, 2^a parte (nivel A).

Continuamos con el capítulo 4, donde veremos que la dilatación del tiempo y la contracción de longitudes son muy evidentes. Estas dos propiedades son equivalentes a las transformaciones de Lorentz y podremos usarlas posteriormente para analizar muchos problemas y situaciones típicas de la R.E.

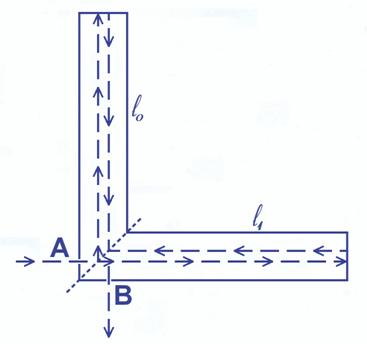
A.4.3.  El interferómetro (y la contracción de longitudes).

La hipótesis de que cualquier observador ve la misma velocidad para la luz nos ha llevado a que el tiempo transcurre a ritmos diferentes para un observador en reposo (S) y otro en movimiento (S’). Algo similar ocurrirá con las medidas de longitudes, pero sólo en la dirección del movimiento.

Para estudiar el efecto de la velocidad sobre las longitudes utilizaremos un instrumento parecido al reloj de luz del apartado anterior, el interferómetro.

Este instrumento es similar (Fig. 4.3) al que usaron Michelson y Morley en 1887 para comprobar las velocidades de la luz en diferentes direcciones y funciona como dos relojes de luz (uno horizontal y otro vertical) sincronizados.

Ambos brazos son iguales y para que vayan sincronizados hacemos entrar un pulso de luz por la entrada A incidiendo sobre un espejo semitransparente (línea oblicua punteada) que deja pasar la mitad de la luz (que seguirá hacia la derecha) y refleja la otra mitad, que saldrá reflejada hacia arriba. Así el rayo de luz que ha entrado por A se ha dividido en dos. Uno sigue en la misma dirección que entró y recorrerá el tubo horizontal (hacia la derecha) hasta chocar con el espejo de la derecha, reflejándose en el y regresando al punto de partida. El segundo rayo o pulso sigue un trayecto vertical a lo largo de un segundo tubo. Cuando alcance el espejo de arriba (final del tubo vertical) se reflejará y regresará también al punto de partida.

Fig. 4.3 -  Interferómetro en reposo.

Supongamos que el hombre que viaja en el tren lleva ahora un interferómetro en la posición de la figura 4.3. El tren viaja de izquierda a derecha (deberemos imaginarlo), y el interferómetro se moverá con el tren en la misma dirección. Durante todo el viaje se mantiene un tubo vertical y el otro horizontal, este último en la misma dirección en la que se mueve el tren.

El sistema funciona como dos relojes de luz (explicados con detalle en las páginas anteriores) que funcionan sincronizados. Ambos brazos miden “c” (desde el espejo semitransparente en que se dividen los rayos hasta el espejo del fondo de cada tubo).

Igual que suponíamos al hablar de relojes de luz, podemos suponer que tras lanzar el primer pulso de luz este va y viene a lo largo de los tubos sin perdida de energía y que unos detectores pueden detectar la llegada de los pulsos de vuelta al espejo semitransparente de la entrada. Unos espejos situados en A y B se encargarían de reflejar de nuevo la luz para que el reloj no se parase y si el reloj tuviera perdidas de energía se podría añadir un mecanismo que renovara el pulso antes de que se extinguiera.

En la literatura relativista se suele seguir la idea de Michelson y Morley, que después del trayecto de ida y vuelta hicieron salir la luz por otro agujero lateral B para medir el desfase de tiempo entre ambas señales. El razonamiento es idéntico tanto si la luz hace un sólo trayecto de ida y vuelta (experimento de Michelson y Morley) como si son dos relojes de luz y los pulsos van y vienen sin parar. En cualquier caso nosotros sólo analizaremos un trayecto de ida y vuelta.

A.4.4.  ¿Qué verá el observador del tren (S’)?

Un experimento casi idéntico a este fue realizado por Michelson y Morley en 1887 con instrumentos muy precisos y observaron exactamente los mismos tiempos en ambos tubos, a pesar de que esperaban que el movimiento de la Tierra hiciera retrasarse al reloj horizontal.

Para él observador de S’ el reloj está quieto, por tanto verá dos pulsos idénticos, uno recorriendo el tubo vertical y otro perfectamente sincronizado recorriendo el tubo horizontal.

Estar sincronizados significa que cuando el pulso vertical llega al final del tubo ocurre lo mismo con el pulso horizontal. Ambos se reflejan a la vez y ambos vuelven hacia atrás a la misma velocidad, llegando simultáneamente al punto de partida (el espejo semitransparente que habíamos colocado junto a la entrada). La Fig. 4.3 representa lo que ve el observador (S’) del tren.

Estudiemos como se ve el interferómetro desde tierra firme y entenderemos la sorpresa de Michelson y Morley en 1887.

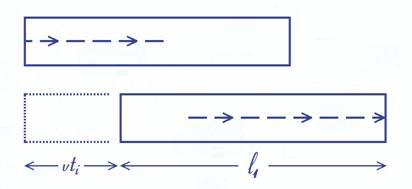
A.4.5.  ¿Qué verá el observador de tierra firme (S)?

Vistos desde tierra los recorridos por ambos tubos resultan ser muy distintos debido precisamente a que están en movimiento.

El recorrido en el tubo vertical es el mismo que en el problema del reloj estudiado en el apartado anterior (Fig. 4.1 para el observador del tren y Fig. 4.2 para el de tierra firme), y por tanto el resultado también será el mismo.

Sin embargo en el trayecto por el tubo horizontal observamos una importante asimetría. Durante el viaje de ida la luz recorre un trayecto mucho más largo, pues el espejo de la derecha se va alejando del pulso de luz.

En la figura 4.4 vemos el tubo horizontal en dos posiciones. Arriba vemos el instante inicial, cuando el pulso de luz sale del espejo semitransparente (no dibujado aquí) hacia la derecha. Abajo el final del primer recorrido, cuando llega al espejo de la derecha. Observamos que el tubo se habrá desplazado un cierto espacio (indicado por la figura punteada de la izquierda) y por tanto el pulso de luz habrá recorrido un espacio más largo que la longitud del tubo. Habrá recorrido la longitud del tubo (representado por l₁) más el espacio que se haya desplazado el tubo (representado por vt_i).

Fig. 4.4 -  Brazo horizontal del interferómetro en movimiento.

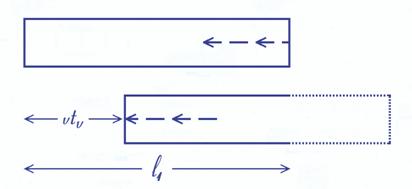
Por el contrario durante el viaje de vuelta el mismo pulso recorre un trayecto mucho más corto debido a que ahora el espejo semitransparente de la entrada corre al encuentro del pulso.

En la figura 4.5 vemos el tubo horizontal en otras dos posiciones. Arriba vemos el principio del viaje de vuelta, justo después de rebotar en el espejo de la derecha. Abajo el final del viaje, cuando llega de nuevo al punto de partida (el espejo semitransparente).

Observamos que el tubo se habrá desplazado un cierto espacio (representado por vt_v) y por tanto el trayecto recorrido es más corto que la longitud del tubo (representada por l₁) y por tanto mucho más corto que el del viaje de ida.

Fig. 4.5 -  Brazo horizontal del interferómetro en movimiento.

Lo primero que nos sorprende es que el observador del tren ha visto tiempos iguales para el trayecto de ida y el de vuelta, mientras el observador de tierra firme ve duraciones muy distintas. Estas situaciones paradójicas son muy frecuentes en relatividad, pero la contradicción es sólo aparente, como veremos más adelante.

A.4.6.  Comparación de los dos trayectos

Para entender mejor lo que ocurre compararemos ahora el trayecto vertical, que conocemos perfectamente (Fig. 4.1 y 4.2), con el trayecto horizontal y lo haremos para ambos observadores.

En la Fig. 4.9 hemos representado los dos trayectos completos, pero comenzaremos estudiando la primera mitad del trayecto, para lo que utilizaremos la Fig. 4.7.

El primer punto a tener en cuenta es que para ambos observadores el movimiento vertical es simétrico. Recordemos que en la Fig. 4.1 esquematizábamos lo que se ve desde el propio tren (S’) y en la  Fig. 4.2  lo que ve el observador de tierra firme (S). Por tanto:

Sabemos que los tiempos medidos por ambos serán diferentes debido a la dilatación temporal, pero para ambos será la mitad de su viaje. Es medio ciclo, la mitad del problema que estamos estudiando.

Para el observador del tren las cosas son muy sencillas pues ambos tubos son iguales y los pulsos que viajan por ellos tienen idénticos comportamientos (Fig. 4.3), de manera que en el instante que estamos analizando, la mitad del tiempo, el observador del tren ve que los dos pulsos llegan simultáneamente al final de ambos tubos. El reloj horizontal y el vertical van perfectamente sincronizados. El segundo medio ciclo, o sea el viaje de regreso de ambos pulsos, también se ve perfectamente sincronizado desde dentro del tren.

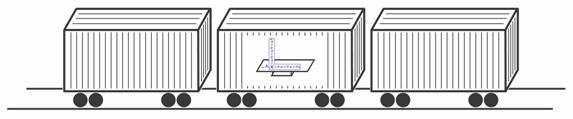
Fig. 4.6 -  El interferómetro y el tren se desplazan a gran velocidad hacia la derecha, pero

dentro del tren no aprecian el movimiento y por tanto ven lo mismo en ambos tubos.

Sin embargo las cosas son más complicadas para el observador de tierra firme.

¿Dónde se encuentra el pulso horizontal cuando el vertical llega al espejo de arriba (o sea a la mitad del tiempo)?

Ya hemos visto que para el observador de tierra firme el trayecto recorrido por la luz es más largo debido a que el tubo se ha desplazado. Queremos saber cuan largo es, pero como hemos decidido no hacer cálculos deberemos hacer un razonamiento geométrico para entender lo que ocurre.

Sabemos que ambos rayos de luz han partido del mismo punto en el mismo instante, por tanto durante esta primera mitad del viaje (tiempos iguales) tienen que haber recorrido la misma distancia, aunque sea en direcciones diferentes (pues la velocidad de la luz es siempre la misma).

Esto es propio de las ondas y para entender lo que pasa podemos tomar como ejemplo cualquier otra onda. Imaginemos por un segundo que tiramos una piedra en el centro de un estanque. Las ondas generadas recorren la misma distancia en todas las direcciones, y esto se refleja en que forman circunferencias a partir del centro en que se originaron. Si en un segundo ha recorrido 5 metros en dirección norte, en dirección este habrá recorrido exactamente lo mismo.

En nuestro interferómetro hemos canalizado estas ondas en dos direcciones y por tanto no vemos las circunferencias, pero podemos coger un compás y trazar una circunferencia desde el punto de partida (el espejo semitransparente) con lo cual podremos comparar los rayos horizontal y vertical (véase la Fig. 4.7).

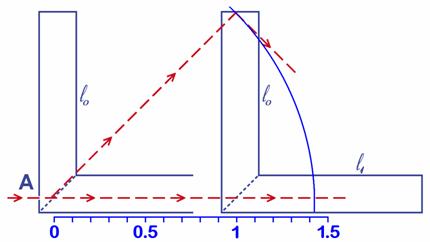
Fig. 4.7-  El rayo vertical llega arriba a la mitad del tiempo. En este tiempo el interferómetro

se ha desplazado una unidad. Pero el pulso horizontal no ha llegado a la mitad del tubo.

En vez de tomar un ejemplo cualquiera hemos elegido la velocidad que nos genera el gráfico más sencillo posible (para este razonamiento geométrico), es la velocidad a la que el tren se desplaza un espacio exactamente igual al brazo vertical del interferómetro (l₀) en el medio ciclo que estamos estudiando (veremos que corresponde a un 71% de la velocidad de la luz, unos 210 000 km/s).

A esta velocidad, tras medio ciclo el pulso vertical está llegando al espejo de arriba. Trazamos con el compás un trozo de circunferencia para ver donde se encuentra el rayo horizontal y obtenemos (ver la cinta métrica de la Fig. 4.7) una distancia de un poco más de 1,4 unidades. Nuestra unidad es l₀, la longitud del brazo (vertical) de nuestro interferómetro.

En ese mismo tiempo el recorrido horizontal del interferómetro es exactamente l₀ (pues hemos elegido la velocidad del tren para que así sea) y la altura a la que ha llegado el rayo vertical también es l₀, de esta manera el rayo vertical (oblicuo en rojo en las Fig. 4.7 y 4.8) recorre exactamente la diagonal de un cuadrado de lado l₀ (una unidad en nuestra cinta métrica), y resulta un gráfico muy fácil de reproducir y de medir con mucha precisión.

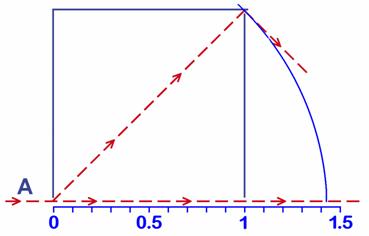
Fig. 4.8 -  El rayo vertical recorre la diagonal de un cuadrado de lado unidad. Es fácil

comprobar con el compás que ambos han recorrido un poco más de 1,4 unidades.

Dado que la longitud del interferómetro era exactamente l₀ tanto horizontal como verticalmente, observamos que cuando el rayo vertical (en rojo) llega arriba el rayo horizontal (también en rojo) todavía no ha llegado a la mitad del tubo, debido a que el tubo se ha movido exactamente esa longitud l₀ .

En la cinta métrica de la figura 4.7 vemos que el interferómetro, y por tanto el punto de partida (el espejo semitransparente) se ha desplazado una longitud exactamente igual a la longitud del tubo vertical ( l₀ ) y por esto se encuentra exactamente sobre el 1 de la cinta.

El pulso de luz se encuentra solamente 0,41 unidades más allá, o sea que no ha llegado a la mitad del tubo horizontal (que serían 0,5 unidades, o sea el punto marcado como 1.5).

Está claro que:

Sin embargo sabemos que el rayo vertical llega de regreso al punto de partida justo en el mismo momento que el rayo vertical, pues así lo ve el observador de dentro del tren (Fig. 4.3).

Cuando se cumpla el tiempo para el observador de tierra firme, el rayo horizontal debería haber llegado al espejo de la derecha y haber regresado al punto de partida, pero hemos visto que el rayo horizontal sólo habrá recorrido un 82 % del tubo horizontal (41 % en cada medio ciclo) y por tanto parece que ni siquiera habrá llegado al final del tubo, y mucho menos habrá regresado a su punto de partida.