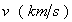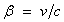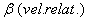A.4. Las transformaciones de Lorentz (nivel A).

Dado que en este nivel introductorio prescindiremos de fórmulas, no llegaremos a escribir las transformaciones de Lorentz, pero veremos que la dilatación del tiempo y la contracción de longitudes son muy evidentes. Estas dos propiedades son equivalentes a las transformaciones de Lorentz y podremos usarlas posteriormente para analizar muchos problemas y situaciones típicas de la R.E.

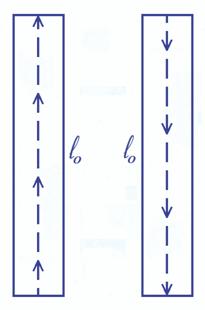
A.4.1.  El reloj de luz

Dentro de la Relatividad Especial todos los relojes son equivalentes, pero el reloj de luz es conceptualmente más sencillo (aunque su realización práctica resultaría complicada) y permite ilustrar el hecho de que observadores distintos verán transcurrir el tiempo a ritmos distintos.

Haciendo los cálculos detallados para este reloj ideal y para un interferómetro ideal se pueden deducir las fórmulas exactas que permiten calcular las medidas que obtendrá un observador a partir de las obtenidas por otro. Estas ecuaciones se conocen como transformaciones de Lorentz y son el primer paso para desarrollar un modelo coherente para la mecánica relativista.

En una primera aproximación (nivel A) no necesitamos llegar a las fórmulas, pero conviene que veamos claramente que los conceptos de espacio y sobre todo el de tiempo quedan profundamente alterados.

Nuestro reloj consiste en un tubo recto y vacío (para que la luz no sea absorbida por el medio) con espejos ideales en los extremos. Si lanzamos un breve pulso de luz de un extremo hacia el otro este pulso viajará de un espejo al otro repetidamente a velocidad constante.

Un detector situado en uno o ambos espejos nos indicará cuando es alcanzado por el pulso de luz, marcando un patrón de tiempo perfectamente regular. Se supone que no hay perdidas de energía, o que existe un mecanismo muy preciso que añade energía al sistema al ritmo adecuado para compensar las posibles perdidas.

En la figura 4.1 vemos a la izquierda el recorrido que hace el pulso de luz en el viaje de ida y a la derecha el trayecto de vuelta.

Como ya sabemos la velocidad de la luz (que se llama “c”) es de unos  300 000 km/s. Esto significa que un rayo de luz tarda poco más de un segundo en ir de la Tierra a la Luna. Es una velocidad impresionante para escalas humanas, pero no para la astronomía, ya que la misma luz tarda 6 horas en llegar a Neptuno y 4 años en llegar a la estrella más próxima.

Fig. 4.1 -  Reloj de luz (ida y vuelta).

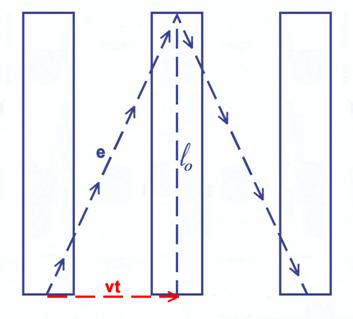
Dado que no necesitamos calcular, con frecuencia usaremos la letra “c” para representar una velocidad igual a la de la luz (300 000 km/s) o para representar una distancia de 300 000 km, y para simplificar más nuestros razonamientos podemos imaginar que la longitud de nuestro reloj es un múltiplo conveniente de c, de manera que el recorrido total de ida y vuelta de la luz sea un número exacto de segundos, por ejemplo un segundo para ir y otro para volver.

A.4.2.  La dilatación temporal

Consideremos ahora un hombre que viaja en un tren (sería más adecuado pensar en un cohete, ya que conviene pensar en elevadas velocidades) llevando un reloj (de luz) y un segundo hombre que le observa desde tierra firme.

Consideraremos que la tierra firme es un sistema de referencia inmóvil (aunque hemos aceptado la hipótesis de que no se puede distinguir un sistema móvil de uno inmóvil) y por tanto inercial (en él se cumplen las leyes de Newton) y lo llamaremos S.

Si el tren se mueve con velocidad constante (v) también será un sistema inercial (en él también se cumplirán las leyes de la mecánica) que llamaremos S’.

¿Cómo se ve correr el tiempo desde estos dos sistemas?

Para centrar ideas supondremos que nuestro reloj tiene una longitud de c (nos referimos a la distancia de 300 000 km), de manera que los trayectos de ida y vuelta de un pulso de luz entre los dos espejos duren exactamente 1 s cada uno.

Para el sistema S’ (para el observador que viaja en el tren) cada ida y vuelta del pulso de luz marca el paso de 1 segundo (Fig. 4.1).

¿Como lo ve el observador de tierra firme S?

Si estamos inmóviles en tierra firme veremos que el rayo de luz hace un trayecto oblicuo debido a que durante el tiempo (t) en que el pulso hace su recorrido, el tubo y el tren se han desplazado una distancia importante ya que suponemos velocidades elevadas. El recorrido de la luz visto desde tierra firme es más largo que el que ve el observador del tren (Fig. 4.2).

Fig. 4.2 -  Reloj de luz en movimiento.

En la figura 4.2 vemos el tubo vertical de nuestro reloj de luz en tres posiciones. A la izquierda en el instante inicial, cuando el pulso de luz parte de abajo. Al cabo de un corto tiempo (1 s) el pulso de luz llega al espejo de arriba, pero el tubo se ha desplazado un cierto espacio (indicado en rojo) y se encuentra en la posición central. Finalmente al cabo de otro tiempo idéntico al anterior (1 s) el pulso de luz regresará abajo, al punto de partida. El instante de llegada abajo está representado por el tercer tubo, el de la derecha.

La primera mitad del recorrido forma un triángulo rectángulo, por lo que se puede aplicar el teorema de Pitágoras para calcular el espacio que recorre este pulso de luz (e) visto desde tierra firme. Aunque no haremos el cálculo, está claro que el observador de tierra firme ve un recorrido mayor (línea oblicua marcada con una “e”) que el observador del tren (Fig. 4.1) que sólo lo ve subir y bajar verticalmente (l₀).

En todo nuestro razonamiento hemos supuesto que el tubo del reloj se mantiene en posición vertical dentro del tren y por tanto perpendicular a la dirección del movimiento. De otra forma sería mucho más complicado comparar lo que se ve desde el tren (Fig. 4.1) con lo que se ve desde tierra firme (el trayecto oblicuo de la Fig. 4.2).

Si ahora tenemos en cuenta la hipótesis de Einstein de que “la velocidad de la luz es la misma en cualquier sistema” resulta evidente que si desde tierra firme se ve un recorrido más largo también se necesita más tiempo para hacerlo. Para el observador S que permanece en Tierra pasa más tiempo, o sea que para el que viaja en el tren pasa menos tiempo.

El hecho de que pase menos tiempo entre dos sucesos es lo mismo que decir que sus unidades de medida se han hecho más grandes y por esto se dice que habla de “dilatación del tiempo”.

Es interesante, para concretar ideas, saber que existe un factor sencillo que se utiliza en R.E. para medir cuanto más rápido pasa el tiempo para el que queda en tierra firme. Este factor se llama factor gamma o constante relativista y se representa por la letra griega gamma ().

Tabla 1 -  Constante relativista () para distintas velocidades.

En la tabla 1 se pueden ver estos valores para una amplia gama de velocidades. El factor gamma es siempre mayor que la unidad pues se obtiene dividiendo el tiempo mayor (el de S) entre el menor (el de S’).

La tabla nos permite ver que a bajas velocidades casi no se notará el efecto, mientras que a altas velocidades la diferencia entre ambos tiempos será muy grande.

En la tabla aparece también la velocidad relativa (), que es la velocidad comparada con la de la luz (c) y siempre será un número entre 0 y 1, ya que la velocidad del móvil no puede superar la velocidad de la luz. En cambio la constante relativista () siempre será mayor que la unidad y crece rápidamente al acercarnos a la velocidad de la luz (300 000 km/s).

Para concretar el significado de la dilatación del tiempo podemos leer algunos valores de esta tabla y compararlos con velocidades conocidas.

La velocidad más rápida en la atmósfera es la de los aviones supersónicos que pueden ir dos o tres veces más rápidos que el sonido, o sea que podemos ir hasta unos 1000 m/s. Es todavía una velocidad muy lenta comparada con la primera que aparece en la tabla, 1000 km/s, y para ésta aun la constante relativista es casi la unidad. La diferencia de 6 millonésimas de segundo es inapreciable para el hombre corriente.

Hay que alcanzar una velocidad de 15 000 km/s para que la diferencia de tiempos sea de una milésima (un segundo en el tren equivale a 1,001252 s en tierra firme).

Para que la diferencia de ritmos sea apreciable a simple vista deberíamos llegar a velocidades del orden de 50 000 km/s, para la cual vemos una diferencia de 14 milésimas (un poco más del 1 %). A partir de aquí el retraso en las comunicaciones y en los relojes se iría haciendo muy evidente.

En los ejemplos se suele usar la velocidad de 180 000 km/s porque tiene una constante relativista especialmente sencilla para los cálculos. En nuestros diagramas utilizaremos este valor.

La diferencia entre los tiempos del tren y de tierra firma es ahora del 25%. Por cada segundo transcurrido en el tren en tierra firme transcurren 1,25 s. Para 100 segundos del tren en tierra firme transcurren 125 s. La diferencia sería claramente apreciable por cualquiera.

Lo que hace interesante este ejemplo es que la diferencia sea exactamente del 25%, ya que en la mayoría de valores de la tabla la constante relativista gamma es sólo aproximada (tiene más decimales).

Como curiosidad, a una velocidad de 290 000 km/s la constante relativista es casi 4, lo cual significa que el tiempo en el tren transcurre 4 veces más lento, o que en tierra firme transcurre 4 veces más rápido. Aunque es una velocidad inalcanzable para el hombre, ya se ha comprobado con partículas atómicas que estas diferencias de ritmos de tiempo son reales.